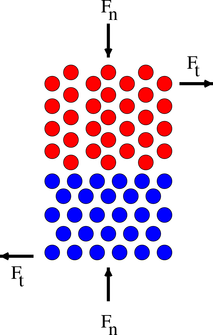
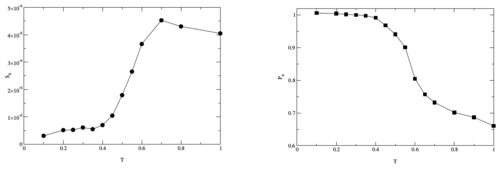
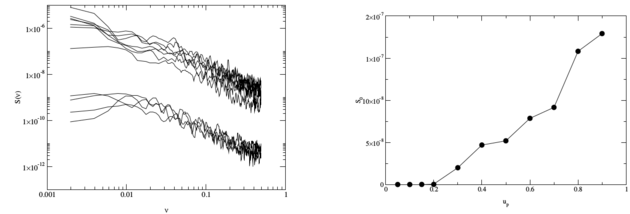
 Figure 4:
Left: Power spectra S(ν) of the percentage of sixfold-coordinated
atoms, P6(t), at velocities up= 0.05 (bottom), 0.1, 0.15, 0.2,
0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9 (top), in a system with 3448 atoms.
A gap in spectral power occurs between up=0.2 and up=0.3.
Right: Spectral power S0 for P6 as a function of sliding velocity
up.
Figure 4:
Left: Power spectra S(ν) of the percentage of sixfold-coordinated
atoms, P6(t), at velocities up= 0.05 (bottom), 0.1, 0.15, 0.2,
0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9 (top), in a system with 3448 atoms.
A gap in spectral power occurs between up=0.2 and up=0.3.
Right: Spectral power S0 for P6 as a function of sliding velocity
up.
|