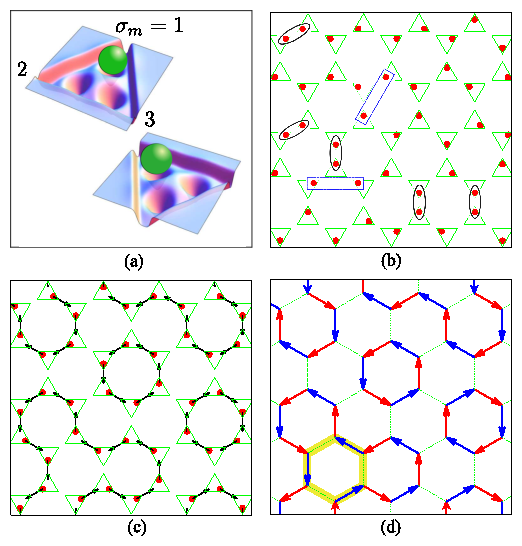
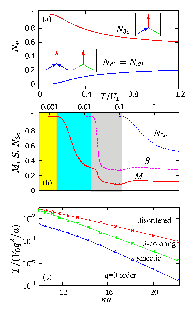
 Figure 3: (a) Nv, the fraction of vertices of type v,
as a function of temperature T/U1.
Upper red line:
N3c;
lower blue line:
Nd1+Nd2;
dashed line: all other vertex types.
Insets: schematics of the three low-temperature vertex types
Nd1, Nd2, and N3c.
(b) Order parameters M and S along with
N3c as a function of temperature T/U1.
The parameter M characterizes a uniform long-range
ordering of particles in which
all loops are directed
in the same direction and parallel to each other.
The stripe order parameter S
describes a partially ordered phase in which
loops are parallel to each other but the direction of
individual loops is disordered.
(c) Phase diagram of temperature T in units of V0q2/a
vs κa showing the
regions in which the ordered, smectic, three-coloring, and disordered
states are observed. Red circles: T3c; green squares: TS;
blue triangles: TN.
Figure 3: (a) Nv, the fraction of vertices of type v,
as a function of temperature T/U1.
Upper red line:
N3c;
lower blue line:
Nd1+Nd2;
dashed line: all other vertex types.
Insets: schematics of the three low-temperature vertex types
Nd1, Nd2, and N3c.
(b) Order parameters M and S along with
N3c as a function of temperature T/U1.
The parameter M characterizes a uniform long-range
ordering of particles in which
all loops are directed
in the same direction and parallel to each other.
The stripe order parameter S
describes a partially ordered phase in which
loops are parallel to each other but the direction of
individual loops is disordered.
(c) Phase diagram of temperature T in units of V0q2/a
vs κa showing the
regions in which the ordered, smectic, three-coloring, and disordered
states are observed. Red circles: T3c; green squares: TS;
blue triangles: TN.
|