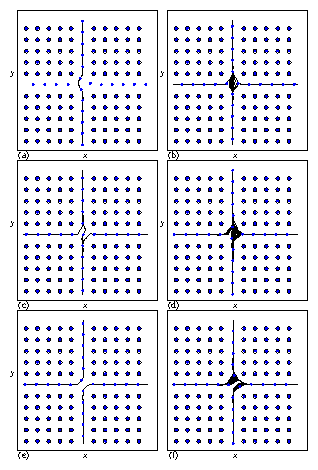
 Figure 1:
Pinning site locations (open circles),
vortex locations (filled dots), and vortex trajectories (lines)
at B=BϕS
for a square pinning array with one row and one column of
pins removed.
The vortex density matches the original square pinning
array density BϕS.
A constant drive of FDy = 0.2 is applied in the y direction and
an increasing drive
FDx is applied in the x direction.
(a) At FDx = 0.025, the vortices in the x channel are
pinned.
(b) At FDx = 0.04, the
vortex trajectories at the intersection are disordered.
(c) At FDx = 0.106 an ordered or coherent flow phase occurs.
(d) Disordered flow at FDx = 0.1105.
(e) Ordered flow at FDx = 0.2.
(f) Disordered flow at FDx = 0.224.
Figure 1:
Pinning site locations (open circles),
vortex locations (filled dots), and vortex trajectories (lines)
at B=BϕS
for a square pinning array with one row and one column of
pins removed.
The vortex density matches the original square pinning
array density BϕS.
A constant drive of FDy = 0.2 is applied in the y direction and
an increasing drive
FDx is applied in the x direction.
(a) At FDx = 0.025, the vortices in the x channel are
pinned.
(b) At FDx = 0.04, the
vortex trajectories at the intersection are disordered.
(c) At FDx = 0.106 an ordered or coherent flow phase occurs.
(d) Disordered flow at FDx = 0.1105.
(e) Ordered flow at FDx = 0.2.
(f) Disordered flow at FDx = 0.224.
|
