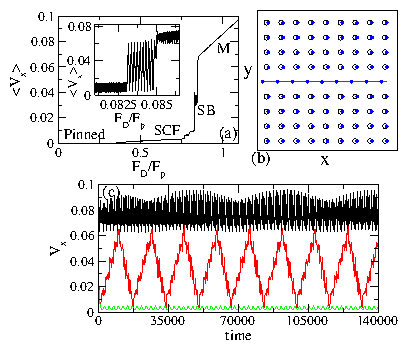
 Figure 1:
(a) The average velocity 〈Vx〉
vs applied force FD/Fp for
a system with
Fp = 0.1,
B/Bϕ = 1.0, and a single removed row of pinning.
Four regimes are marked: a pinned regime, a single channel flow
(SCF) regime, a shear banding (SB) regime,
and a moving (M) phase in which all of the vortices are flowing.
Inset: A blowup of the main panel
for 0.081 ≤ FD/Fp ≤ 0.0865 in the shear banding phase
where a short time average is used for the velocities
so that the fluctuations can be seen more clearly.
Large scale oscillations occur as the system switches back and forth
between three moving rows of vortices and all rows of vortices moving.
On a long time average, the oscillating regime has an intermediate
value of 〈Vx〉 as shown in the main panel.
(b) The vortex positions (dots), trajectories (lines), and
pinning site locations (open circles)
for a small subsection of the sample in (a)
in the SCF phase at FD/Fp = 0.6.
(c) Vx vs time for the system in (a)
at FD/Fp = 0.7, 0.85, and 0.92 (from bottom to top).
Figure 1:
(a) The average velocity 〈Vx〉
vs applied force FD/Fp for
a system with
Fp = 0.1,
B/Bϕ = 1.0, and a single removed row of pinning.
Four regimes are marked: a pinned regime, a single channel flow
(SCF) regime, a shear banding (SB) regime,
and a moving (M) phase in which all of the vortices are flowing.
Inset: A blowup of the main panel
for 0.081 ≤ FD/Fp ≤ 0.0865 in the shear banding phase
where a short time average is used for the velocities
so that the fluctuations can be seen more clearly.
Large scale oscillations occur as the system switches back and forth
between three moving rows of vortices and all rows of vortices moving.
On a long time average, the oscillating regime has an intermediate
value of 〈Vx〉 as shown in the main panel.
(b) The vortex positions (dots), trajectories (lines), and
pinning site locations (open circles)
for a small subsection of the sample in (a)
in the SCF phase at FD/Fp = 0.6.
(c) Vx vs time for the system in (a)
at FD/Fp = 0.7, 0.85, and 0.92 (from bottom to top).
|
