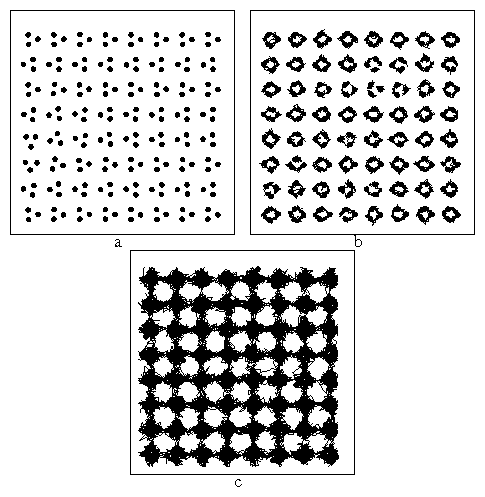
Figure 1: The colloid configurations (black dots) at T=0.0 for a square
2D periodic substrate with A=2.5, for a half-integer colloidal
density, Nc=1.5 Nm. Every other minima captures a single colloid,
while the remaining minima capture two colloids in a dimer state. There is
no long-range rotational order of the dimers.
Figure 1: The colloid configurations (black dots) at T=0.0 for a square
2D periodic substrate with A=2.5, for a half-integer colloidal
density, Nc=1.5 Nm. Every other minima captures a single colloid,
while the remaining minima capture two colloids in a dimer state. There is
no long-range rotational order of the dimers.
|