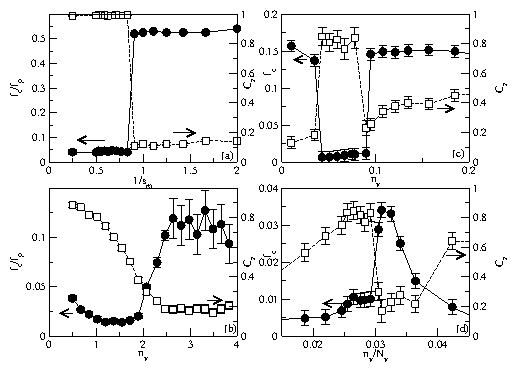
 Figure 2: (a) fc versus nv for a sample with Nv=4, L=8, and
fp=0.04f0*
at temperatures of fT=0.0005 (circles), fT=0.1 (squares),
fT=0.2 (diamonds), and fT=0.3 (triangles).
(b) Cz corresponding to panel (a).
(c) Vx versus fT for the same sample, at a fixed drive
of fd=0.1f0*, for fields nv= 0.061, 0.083, 0.108, 0.133, and 0.178.
(d) Cz corresponding to panel (c). Inset to (c): Vx versus fT
for a sample with Nv=80, nv=2.0,
L=16, np=8.0, and fp=0.1f0*.
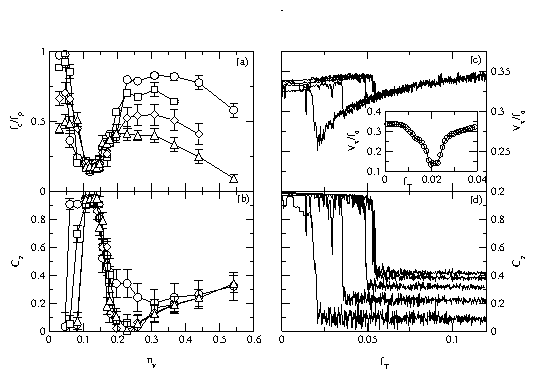
Figure 2: (a) fc versus nv for a sample with Nv=4, L=8, and
fp=0.04f0*
at temperatures of fT=0.0005 (circles), fT=0.1 (squares),
fT=0.2 (diamonds), and fT=0.3 (triangles).
(b) Cz corresponding to panel (a).
(c) Vx versus fT for the same sample, at a fixed drive
of fd=0.1f0*, for fields nv= 0.061, 0.083, 0.108, 0.133, and 0.178.
(d) Cz corresponding to panel (c). Inset to (c): Vx versus fT
for a sample with Nv=80, nv=2.0,
L=16, np=8.0, and fp=0.1f0*.
|