Physical Review E 75, 011403 (2007)

Point-defect dynamics in two-dimensional colloidal crystals

A. Libál1,2, C. Reichhardt1, and C.J. Olson Reichhardt1

1Center for Nonlinear Studies and Theoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
2Department of Physics, University of Notre Dame, Notre Dame, Indiana 46556, USA

(Received 26 September 2006; published 11 January 2007)

We study the topological configurations and dynamics of individual point defect vacancies and interstitials in a two-dimensional crystal of colloids interacting via a repulsive Yukawa potential. Our Brownian dynamics simulations show that the diffusion mechanism for vacancy defects occurs in two phases. The defect can glide along the crystal lattice directions, and it can rotate during an excited topological transition configuration to assume a different direction for the next period of gliding. The results for the vacancy defects are in good agreement with recent experiments. For interstitial point defects, which were not studied in the experiments, we find several of the same modes of motion as in the vacancy defect case along with two additional diffusion pathways. The interstitial defects are more mobile than the vacancy defects due to the more two-dimensional nature of the diffusion of the interstitial defects.
I. INTRODUCTION
II. SIMULATION METHODS
III. POINT DEFECT CONFIGURATIONS
IV. DEFECT MOTION AND LOCAL BURGERS VECTOR DIRECTIONS
A. Isotropic temperature
B. Anisotropic temperature
V. PROPERTIES OF THE DEFECT DIFFUSION
A. Differences in defect diffusion for vacancies and interstitials
B. Probability of different defect configurations
VI. DISCUSSION
VII. CONCLUSIONS
References


I.  INTRODUCTION

Topological defects in two-dimensional crystals are relevant to a number of condensed matter systems including vortices in type-II superconductors [1], Wigner crystals [2], magnetic bubble arrays [3], atoms on surfaces, and dusty plasmas [4]. The creation of topological defects such as dislocations and disclinations leads to a two step melting process and an intermediate hexatic phase [5,6,7]. Topological defects play a role in the mechanical response of the system, such as when a shear is applied to the crystal, and also determine how effectively the crystal can be pinned to a disordered substrate. More recently, there has been growing interest in studying topological defects in two-dimensional systems on curved surfaces, such as colloidal particles on the surface of a liquid drop [8,9]. In addition to providing insight into how defects can affect equilibrium and nonequilibrium properties of these systems, understanding how individual topological defects move would also be valuable for technological applications, such as the nanoscale or mesoscale engineering of new two-dimensional materials.
In an effort to understand the dynamics of individual point defects in two dimensions, recent experiments were conducted in which point defects were artificially created in a two-dimensional colloidal suspension by manipulating the colloids with optical tweezers [10,11,12]. Here, a defect is created by removing one or two colloids from a perfect triangular lattice, resulting in a mono- or divacancy. The defect configurations were shown to have a lower symmetry than the triangular lattice, and specific topological arrangements were characterized by the arrangement of fivefold and sevenfold coordinated colloids around the cores of the mono- and divacancies. The experiments showed that the trajectories of both types of defects followed the major axis directions of the triangular colloidal crystal. As a result, at short times the defect diffusion had one-dimensional characteristics.
In this work, we examine the topological configurations and dynamics of single point vacancies and interstitial colloids in a two-dimensional triangular colloidal crystal. Only vacancies were considered in the experimental work [10,11,12], but here we compare the behavior of vacancies to that of interstitial defects. We find that the point defects have numerous stable topological configurations as well as several frequently appearing excited configurations. The diffusive thermal motion of the defects is aligned with the major axes of the crystal, as also seen in the experiments. As the defect moves, it switches between gliding configurations, which contain two fivefold coordinated particles, and transient configurations, which contain three or more fivefold coordinated particles. The defect is able to change its gliding orientation in the transient configurations. The mobility of interstitial defects is greater than that of vacancy defects, and we show that this is a result of the fact that interstitial defects are more likely to undergo reorientations in their gliding direction than vacancy defects, giving the diffusion of the interstitial defects a more two-dimensional character. We discuss the implications of our work for other systems, such as the effect of the motion of interstitial and vacancy defects on transport in two-dimensional vortex lattices.

II.  SIMULATION METHODS

We simulate a two dimensional colloidal crystal composed of N=1116±1 particles using Brownian dynamics. The system size is Lx=31a0 and Ly=18√3a0, where distances are measured in units of the colloid lattice constant a0, and where we employ periodic boundary conditions in both the x and the y directions. The overdamped equation of motion for an individual colloid i is
η dri
dt
 = fi = fcc + fiT
(1)
where the damping coefficient η = 1 in simulation units. Here the colloid-colloid interaction force is fcc = −∑j ≠ iN ∇i U(rij)∧rij, where rij=|ri−rj| is the distance between particles located at ri and rj, and ∧rij=(ri−rj)/rij. We represent the colloid interaction via a Coulomb potential that is screened by the presence of ions in the liquid phase, giving us the Yukawa form U(rij) = E0 q2 exp(−κrij)/rij. The unit of energy is E0=Z*2/(4πϵϵ0 a0) where Z* is the unit of charge, ϵ is the solvent dielectric constant, q=1 is the dimensionless charge on each colloid, and 1/κ = 0.16 a0 is the screening length. Our system is in the strongly charged low volume fraction limit, allowing us to neglect hydrodynamic interactions. The thermal force fiT is introduced as Langevin random kicks that obey the equations 〈fiT(t)〉 = 0 and 〈fiT(t)fjT(t′)〉 = 2ηkB T δijδ(t−t′). Temperatures are reported with respect to the melting temperature fTm for the two-dimensional crystal. Throughout this work, we consider temperatures in the range 0.37 ≤ fT/fTm ≤ 0.62, which is high enough to produce observable defect motion, but low enough to fall below the temperature at which a proliferation of fivefold and sevenfold defect excitations begins to occur. After initializing the system in a triangular lattice, we either add or subtract a single colloid from a location near the center of the sample. We then measure the time evolution of the system over a long time period of 2 ×108 simulation time steps.
The periodic boundary conditions in our sample prevent the individual defects from annihilating. Since the interaction between topological defects is well known to be long ranged, finite size effects are always a concern in a periodic system. This is particularly important in studies of multiple interacting defects. In our case, we are working with only a single defect, which experiences a perfectly symmetrical interaction with its images across the periodic boundaries. This tends to minimize the impact of the periodic boundaries. To check for finite size effects, we tested larger systems and did not observe any changes in the diffusive behavior. Additionally, our results for the vacancy defects are in good agreement with experiments, offering further evidence that we have avoided finite size effects.

III.  POINT DEFECT CONFIGURATIONS

To characterize the defect configuration and identify the position of the defect, we use a Voronoi cell construction performed after the system has relaxed into a stationary state from its initial configuration. We can identify the coordination number zi of each colloid by counting the sides of the polygons in the Voronoi construction. In an ideal triangular lattice, all particles are sixfold coordinated with zi=6. Our system has either a missing particle or an extra particle, and the defect core is surrounded by a number of zi ≠ 6 particles. We identify distinct topological configurations of the defect based on the Voronoi cell picture, adopting the same notation as used in Refs. [11,13]. All of the possible configurations that exist in this system conserve the average sixfold coordination of the particles,
N
∑
i=1 
 zi = 6N .
(2)
Fig1.png
Figure 1: Voronoi cell construction for commonly observed vacancy defect configurations. Colloid positions are indicated by dots. The Voronoi cells are colored according to the coordination number zi of the colloids: white, zi=6; light grey, zi=7; dark grey, zi=5; very dark grey, zi=8. Only a 6 a0 ×6 a0 portion of the full system is shown. (a) A twofold crushed vacancy (V2a). (b) A split vacancy (SV) centered on a zi=8 colloid. (c) A threefold symmetric vacancy (V3). (d) A fourfold symmetric excited configuration V′4 containing eight colloids with zi ≠ 6.
In Fig. 1 we illustrate the most prevalent configurations for the vacancy defect. Fig. 1(a) shows that the twofold crushed configuration (V2a) consists of two nearly parallel pairs of zi=5 and zi=7 particles. The split configuration (SV) for the vacancy, illustrated in Fig. 1(b), contains three particles with zi ≠ 6, forming an almost straight line with two zi=5 particles on opposite sides of a zi=8 particle. The third equilibrium configuration for the vacancy, the threefold symmetric configuration (V3) shown in Fig. 1(c), consists of three pairs of particles with zi=5 and zi=7 arranged around the outside of a triangle that is centered on the vacancy. These configurations are the same as those observed for the monovacancy in the colloidal experiments [11,12]. Figure 1(d) illustrates an important excited configuration that we find for the vacancy. This fourfold symmetric configuration, termed V′4, contains eight colloids with zi ≠ 6. It is short lived and plays a role in the mobility of the vacancy, as will be described below.
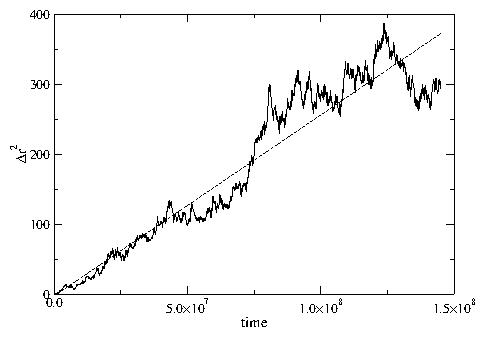
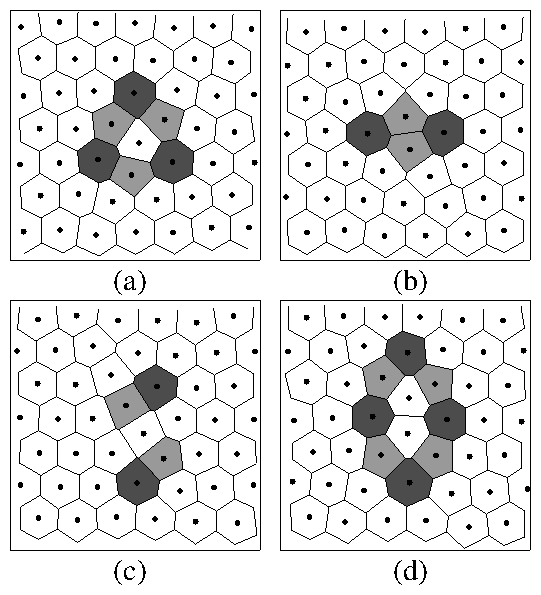
Fig2.png
Figure 2: Voronoi cell construction for commonly observed interstitial defect configurations. Colloid positions are indicated by dots. The Voronoi cells are colored according to the coordination number zi of the colloids: white, zi=6; light grey, zi=7; dark grey, zi=5. Only a 6a0 ×6a0 portion of the full system is shown. (a) A threefold symmetric interstitial, I3. (b) A twofold symmetric interstitial, I2. (c) A disjoint twofold symmetric interstitial, I2d. (d) A fourfold symmetric excited configuration I′4.
Figure 2 shows the main configurations for the interstitial defect. Fig. 2(a) illustrates a threefold symmetric interstitial, I3, composed of a triangular arrangement of zi=5 and zi=7 colloids centered around the interstitial. A twofold symmetric interstitial configuration, I2, appears in Fig. 2(b). This configuration can split to become a disjoint twofold symmetric interstitial, I2d, shown in Fig. 2(c). The interstitial defect forms an excited configuration that is similar in form to that seen for the vacancy defect. Termed a fourfold symmetric excited configuration, I′4, this interstitial configuration is shown in Fig. 2(d). As in the vacancy case, this excited configuration persists only for short times, but as we describe in Section V.B, it plays an important role in the motion of the defect.

IV.  DEFECT MOTION AND LOCAL BURGERS VECTOR DIRECTIONS

To study the motion of the two types of defects, we must identify the location of each defect. We define the defect position rd to be at the center of the Nzi ≠ 6 colloids with zi ≠ 6 that are present in the system,
rd= 1
Nzi ≠ 6
 N
∑
i=1 
 ri(1−δ(zi−6)) .
(3)
With this measure, we can follow the trajectories of a defect under thermal diffusion.
Fig3.png
Figure 3: Diffusion of a vacancy defect at fT/fTm=0.4. Only a 14a0 ×14a0 portion of the full system is shown. Dark lines: trajectory followed by the vacancy over a period of 4.3 ×107 time steps. Light lines: long-time average location of the crystalline lattice through which the vacancy is moving. Over short times, the vacancy diffuses in the directions of the major axes of the crystal.

A.  Isotropic temperature

In Fig. 3 we illustrate the trajectory of a vacancy defect over a period of t=4.3 ×107 simulation time steps at a temperature of fT/fTm = 0.4. We also indicate the time-averaged location of the background triangular lattice to show that the defect diffusion follows the main crystalline lattice directions, [1 0], [0 1] and [―1 1]. The defect diffuses by gliding along the lattice directions in a one-dimensional random walk, punctuated by occasional reorientation transitions. This suggests that at short times the diffusive motion has one-dimensional characteristics, while for long times the diffusion is isotropic. The trajectories we observe are very similar to those found in the vacancy experiments of Ref. [10] where the defect moved along the symmetry directions of the crystal. We find that interstitial defects move in a similar manner. The reorientation transitions that occur during diffusion are mediated by the formation of either a threefold symmetric configuration or one of the excited configurations illustrated in Figs. 1 and 2. We describe the reorientations in more detail below.
In order to characterize the motion along the different crystalline axis, we require a definition of the orientation of the defect as a function of time. The orientation of a dislocation is readily obtained using the Burgers vector b; however, a point defect has a net Burgers vector of b=0. We can construct local Burgers vectors bjl by associating each of the Nzi=5 colloids that have zi=5 with the closest zi > 6 colloid to form a dislocation, such that each zi=7 colloid is paired with only one zi=5 colloid, and under the constraint that the total length, ∑j=1Nzi=5|bjl|, is minimized.
Fig4.png
Figure 4: (a) Time series of the orientations α1 (upper dark line) and α2 (lower dashed line) determined from the two local Burgers vectors b1l and b2l in the gliding vacancy defect configurations SV and V2a for a system with fT/fTm=0.4. (b) From the same system, a polar plot of the probability P(α) of observing a vacancy defect oriented at an angle α with respect to the zero x axis.
The twofold symmetric configurations, V2a, I2, and I2d, along with the split vacancy configuration SV, all have only two local Burgers vectors bjl which are close to being parallel to each other. For these configurations, which we refer to as gliding configurations, we define the orientation of the defect to be in the direction perpendicular to one of the local Burgers vectors. We also identify the angle αj which each Burgers vector makes with the zero y axis. In Fig. 4(a) we plot the time series of α1 and α2 for a system with a vacancy defect diffusing at fT/fTm=0.4. The angles are only defined during the time periods when the vacancy is in the configuration V2a or SV, but the vacancy spends most of the time in one of these two configurations, which have |α1−α2| ≅ π. Figure 4(a) shows that α1 and α2 remain fixed at a particular angle for extended periods of time, punctuated by relatively rapid changes to a new angle. A histogram of the α values with both α1 and α2 combined, plotted in polar coordinates in Fig. 4(b), indicates that α is correlated with the six directions of the crystal lattice. Within our sampling error, all six of the angles appear with equal probability.

B.  Anisotropic temperature

Many two-dimensional systems contain some type of anisotropy which could originate in the particle-particle interactions or from an underlying weak periodic substrate modulation [14,15,16]. Since we found that the defects move along the symmetry directions of the crystalline lattice, it may be expected that if some form of anisotropy is added, the motion may be more prominent along certain directions. A similar system has recently been realized experimentally in a colloidal system composed of superparamagnetic particles [17]. With the application of an external magnetic field, the interactions between the colloids could be made anisotropic. As a result, dislocations formed in the system with a preferred orientation, resulting in melting along the direction of the applied magnetic field.
Fig5.png
Figure 5: P(α), the histogram of α values observed during a simulation run, for different temperature anisotropies in a system with a vacancy defect. In all cases fTy/fTm=0.62. Thick continuous line: fTx/fTy=0.1, dotted line: fTx/fTy=0.3, dashed line: fTx/fTy=0.5, and thin continuous line: fTx/fTy=0.7.
We consider the effect of adding an anisotropic temperature to our system by setting fTx/fTy < 1, where fTy is fixed at fTy/fTm=0.62. Under these conditions, the symmetric diffusion disappears and the defects move preferentially in one direction. In Fig. 5 we plot P(α) for several different temperature anisotropy ratios. As fTx/fTy is decreased from 1, the value of P(|α = π/2|) increases dramatically while P(α) for the other four crystal directions decreases. This indicates that the defect spends most of the time with α oriented along the y direction, meaning that the local Burgers vector is oriented along the x direction. Reorientation transitions for the defect occur much less frequently than in the isotropic case, causing the defect to undergo one-dimensional diffusion for much longer periods of time, and resulting in a highly anisotropic diffusion over time. Such anisotropic diffusion is consistent with the results obtained in the experiment of Ref. [17].

V.  PROPERTIES OF THE DEFECT DIFFUSION

We have shown that the defect trajectory follows the main crystalline directions. The mechanism of defect motion is primarily a gliding process. In the case of a vacancy defect, the vacancy can glide in the configurations SV or V2a, which have parallel local Burgers vectors and a well-defined glide direction. The one-dimensional gliding motion is interspersed with direction switching transitions that occur by means of the V3 configuration or the excited V′4 configuration. Both of these configurations have higher symmetry than the gliding configurations but also have nonparallel local Burgers vectors, and hence no well-defined glide direction. Thus, when the vacancy enters a transition configuration, the symmetry breaking that defined a glide direction is lost. The vacancy spends a relatively short time in the transition configuration before reentering one of the glide configurations, which may have the same or a different glide orientation than the glide configuration which preceded the transition configuration. The high symmetry of the transition configurations permit the defect to reorient its direction of motion along a new lattice direction. Interstitial defects undergo similar sequences of gliding and reorientation, with the I2 and I2d configurations providing the gliding motion, and the I3 and I′4 configurations permitting the reorientation.
The vacancy position remains stationary when entering a transition configuration such as V3, but the position of the interstitial shifts slightly when switching between the I2 or I2d and I3 configurations, providing an additional mechanism for interstitial motion that does not exist for the vacancy defect. It is also possible for interstitial motion to occur through a `breathing' process caused by transitions between the I3 and I′4 configurations.
Fig6.png
Figure 6: (a) Histograms of the discrete jumps ∆x (solid line) and ∆y (dashed line) for a vacancy defect. (b) Histograms of the discrete jumps ∆x (solid line) and ∆y (dashed line) for an interstitial defect. In this figure, the jump distances are measured in their natural units. ∆x is given in units of a0, and ∆y is given in units of √3a0/2
We highlight the difference in the mobility mechanisms for the two types of defects by measuring the individual jumps of the defects from one lattice position to the next. We define ∆xi=(rd,i(t+dt)−rd,i(t)) ·∧x and ∆yi=(2/√3)(rd,i(t+dt)−rd,i(t)) ·∧y, where we take dt=200 simulation time steps. Histograms of both ∆x and ∆y are plotted in Fig. 6(a) for a vacancy defect and in Fig. 6(b) for an interstitial defect. The vacancy defect moves only by a glide mechanism. The process of switching between V2a and SV translates the defect center by half a lattice constant along one of the main crystal axis directions. This produces four non-zero values of ∆x, ±cos(0)/2 and ±cos(π/3), and two non-zero values for ∆y, ±sin(π/3)/√3. Since we are plotting the histogram of both ∆x and ∆y in their natural units, which are a0 and √3a0/2 respectively, we observe peaks at ∆x=±0.25 and ±0.5 and at ∆y=±0.5 in Fig. 6(a). The same peaks appear for the interstitial defect in Fig. 6(b) since the gliding mechanism also operates in this case, but there are now additional peaks in ∆x and ∆y. These peaks are produced by the other two processes that can move the interstitial defect: the switch between the I2 or I2d and I3 configurations, and the breathing motion between the I3 and I′4 configurations. These two processes move the defect center half a lattice constant along directions that lie between the main crystalline directions, at π/6, π/2, 5π/6, 7π/6, 3π/2, and 11π/6. The result is peaks at ∆x = ±cos(π/6)/2 ≅ ±0.43 and peaks at ∆y = ±sin(π/6)/√3 ≅ ±0.29 and ∆y = ±2sin(π/6)/√3 ≅ ±0.58.

A.  Differences in defect diffusion for vacancies and interstitials

Fig7.png
Figure 7: ∆r2 versus time showing the diffusion of the vacancy defect at fT/fTm=0.62. The dashed line is a linear fit, consistent with linear two-dimensional diffusion.
Fig8.png
Figure 8: Diffusion constant D as a function of temperature fT/fTm. Filled circles: vacancy defect. Open triangles: interstitial defect.
For short times, the defect trajectory follows the main crystalline directions, as was shown in Fig. 3. On the longer time scales, however, we find a linear diffusive behavior when we measure the distance that the defect has traveled from its original location as a function of time, ∆r2 = |rd(t)−rd(0)|2. This quantity is plotted in Fig. 7 for a vacancy defect at fT/fTm=0.4. We find that ∆r2 increases linearly with time, as indicated by the fit in the figure. Linear diffusion of monovacancies was also observed in the experiments of Ref. [10].
To compare the mobility of interstitial and vacancy defect, we measure the diffusion constant D, given by
D= 
  		|rd(t+dt)−rd(t)|
dt
 
  		,
(4)
with dt=200 simulation time steps, at a series of temperatures for each defect type. The results are plotted in Fig. 8. The diffusion constant increases with temperature in each case. Importantly, the interstitial defect diffuses significantly faster than the vacancy defect at all temperatures.

B.  Probability of different defect configurations

Fig9.png
Figure 9: (a) Probability to observe different defect configurations for the vacancy defect. Open circles: P(SV)+P(V2a); filled squares: P(V3); open triangles: P(V′4). (b) Probability to observe different defect configurations for the interstitial defect. Filled squares: P(I3); open circles: P(I2)+P(I2d); open triangles: P(I′4).
To help account for the faster diffusion of the interstitial defect compared to the vacancy defect, we compare the time the defects spend in the different topological configurations. In Fig. 9(a) we plot the probability P of observing each configuration as a function of temperature fT/fTm for the vacancy defect, and compare this to Fig. 9(b) which shows the probability of observing interstitial defect configurations versus temperature.
Figure 9(a) shows that the vacancy defect spends most of the time in the split (SV) and the twofold crushed (V2a) configurations, which both allow for gliding motion. The excited configuration V′4 occurs very infrequently and does not contribute significantly to the diffusive process. As the temperature increases, the transition states V3 and V′4 occur with greater probability, indicating that the defect can reorient more easily. A greater number of defect reorientations combined with higher thermal excitation leads to a higher diffusion constant at higher temperature. Since the gliding motion is one-dimensional, the defect can only move away from its starting position as rapidly as a one-dimensional random walk if no reorientation occurs. Reorientation of the glide direction produces a more two-dimensional diffusion which allows the defect to move away more rapidly from its starting position.
The interstitial defect spends much more time in the transition configuration I3 than in any other configuration, as indicated in Fig. 9(b). The excited I′4 configuration for the interstitial defect also appears with much higher probability than the excited V′4 configuration for the vacancy defect case. Overall, this produces a much higher probability for reorientation of the direction of motion of the interstitial defect, and makes its diffusion more two-dimensional than that of the vacancy defect at all temperatures considered here. The result is a greater mobility of the interstitial with respect to the vacancy.

VI.  DISCUSSION

An open question is how general our results are for defect motion in other two-dimensional systems where the particles have different types of interaction potentials. Although it is beyond the scope of this paper to address this issue in detail, we believe that our results should hold for any two-dimensional system with relatively soft particle-particle interactions in which the ground state is a triangular lattice. Very short range potentials, such as hard sphere interactions, are likely to produce significantly different behavior. It is possible for two-dimensional systems to have some other type of ordered ground state, such as a square or rectangular lattice. These lattices have different available gliding directions compared to the triangular lattice, so there could be either fewer or more modes of motion available to the defects. This would be an interesting issue to explore in the future.
Our results could have some implications for the mobility of defects in other two-dimensional systems where the number of vacancies or interstitials can be carefully controlled, such as superconducting vortices [18,19] or colloids [20] interacting with periodic substrates. At particle densities where there is one particle per substrate minimum, termed a matching density, the system is free of topological defects, while vacancies appear for slightly lower particle densities and interstitial defects form at slightly higher particle densities. If the interstitial defects remain more mobile than vacancy defects in the presence of a substrate, the interstitials should depin more readily than the vacancy defects. In the case of superconducting vortices, this would imply that the critical current drops off more rapidly above the matching density (when interstitials are present) than below the matching density (when vacancies are present). This is agreement with earlier observations [19].
Vacancy and interstitial defect motion has also been studied in three-dimensional systems in the context of atomic crystals. Such systems are not only massive, making them sensitive to vibrational modes, but also can form a variety of different lattice structures depending on the details of the atomic interactions. A convenient method for producing isolated vacancies or interstitials in an atomic crystal is through ion damage processes. We note that in this context, unusually high mobility of self-interstitial atoms (SIAs) has been observed and attributed to the high likelihood of rotational motions for the dumbbell atomic configurations associated with the SIA [21]. Although the dimensionality of the resulting motion is different, this resembles our observation that interstitial defects are more mobile than vacancy defects due to the greater likelihood of defect reorientation.
Another issue is the relative stability of interstitial and vacancy defects. Due to the geometry of our system, which has periodic boundary conditions, both the interstitial and vacancy defects are completely stable since there is no free surface where the defects can annihilate. In a real crystal, the more mobile species of defect will reach the edge more rapidly and annihilate. Thus, one implication of the faster mobility of interstitial defects is that a crystal that forms with an initial population of vacancy and interstitial defects will, over time, experience a greater loss of interstitial defects to the crystal edge compared to vacancies, particularly if there is a strain field that helps drive the defects to the edge. Both interstitials and vacancies can still annihilate within the crystal, but the difference in edge annihilation could result in a dominant population of the slower moving vacancy defects in the relaxed crystal.

VII.  CONCLUSIONS

In summary, we have studied the topological configurations and dynamics of individual vacancy and interstitial defects in a triangular two dimensional colloidal crystal. We use a Voronoi cell construction to characterize the different topological configurations assumed by the defects. For vacancy defects, we find the same configurations that were observed in recent experiments. We show that interstitial defects, which were not studied in the experiment, appear in distinct configurations and have a significantly higher mobility than the vacancy defects. The mobility is affected by short lived excited configurations which have four or more fivefold or sevenfold coordinated colloids surrounding the defect. The defect diffusion process is one dimensional at short time scales when the defects glide along the symmetry directions of the crystal. Periodically, the defects enter a transition configuration which has higher symmetry than the glide configuration. This permits the defect to reorient its glide direction when it returns to a glide configuration after a short period of time. As a result of these reorientations, linear two-dimensional diffusion occurs in the long time limit. Application of an anisotropic temperature causes the diffusion process to favor one of the permitted gliding directions. We describe the mechanisms of defect translation in detail, and show that the vacancy defect has one mode of motion, but the interstitial defect has three. It is these additional modes of motion that give the interstitial defect a has a much higher probability of undergoing a reorientation transition than the vacancy defect at a given temperature, causing the interstitial diffusion to be more two-dimensional in character and therefore faster.

8  Acknowledgments

We thank Z. Nussinov, A.F. Voter, and G. Zimányi for useful discussions. This work was carried out under the auspices of the National Nuclear Security Administration of the U.S. Department of Energy at Los Alamos National Laboratory under Contract No. DE-AC52-06NA25396.

References

[1]
E. Frey, D.R. Nelson, and D.S Fisher, Phys. Rev. B 49, 9723 (1994).
[2]
D.S. Fisher, B.I. Halperin, and R. Morf, Phys. Rev. B 20, 4692 (1979).
[3]
R. Seshadri and R.M. Westervelt, Phys. Rev. Lett. 66, 2774 (1991).
[4]
R.A. Quinn and J. Goree, Phys. Rev. E 64, 051404 (2001).
[5]
D.R. Nelson, Defects and Geometry in Condensed Matter Physics (Cambridge Univ. Press, Cambridge, 2002).
[6]
For a review see K.J. Strandburg Rev. Mod. Phys. 60, 161 (1988).
[7]
K. Zahn, R. Lenke, and G. Maret, Phys. Rev. Lett. 82, 2721 (1999).
[8]
A.R. Bausch, M.J. Bowick, A. Cacciuto, A.D. Dinsmore, M.F. Hsu, D.R. Nelson, M.G. Nikolaides, A. Travesset, and D.A. Weitz, Science 299, 1716 (2003).
[9]
P. Lipowsky, M.J. Bowick, J.H. Meinke, D.R. Nelson, and A.R. Bausch, Nature Materials 4, 407 (2005).
[10]
A. Pertsinidis and X.S. Ling, Nature 413, 147 (2001).
[11]
A. Pertsinidis and X.S. Ling, Phys. Rev. Lett. 87, 098303 (2001).
[12]
A. Pertsinidis and X.S. Ling, New J. Phys. 7, 33 (2005).
[13]
S. Jain and D.R. Nelson, Phys. Rev. E 61, 1599 (2000).
[14]
A. Chowdhury, B.J. Ackerson, and N.A. Clark, Phys. Rev. Lett. 55, 833 (1985).
[15]
Q.-H. Wei, C. Bechinger, D. Rudhardt, and P. Leiderer, Phys. Rev. Lett. 81, 2606 (1998).
[16]
L. Radzihovsky, E. Frey, and D.R. Nelson, Phys. Rev. E 63, 031503 (2001).
[17]
C. Eisenmann, U. Gasser, P. Keim, and G. Maret, Phys. Rev. Lett. 93, 105702 (2004).
[18]
K. Harada, O. Kamimura, H. Kasai, T. Matsuda, A. Tonomura, and V.V. Moshchalkov, Science 274, 1167 (1996); S.B. Field, S.S. James, J. Barentine, V. Metlushko, G. Crabtree, H. Shtrikman, B. Ilic, and S.R.J. Brueck, Phys. Rev. Lett. 88, 067003 (2002); A.N. Grigorenko, S.J. Bending, M.J. Van Bael, M. Lange, V.V. Moshchalkov, H. Fangohr, and P.A.J. de Groot, ibid. 90, 237001 (2003).
[19]
C. Reichhardt, J. Groth, C.J. Olson, S.B. Field, and F. Nori, Phys. Rev. B 54, 16108 (1996); C. Reichhardt, C.J. Olson, and F. Nori, ibid. 57, 7937 (1998); C. Reichhardt and N. Grønbech-Jensen, ibid. 63, 054510 (2001).
[20]
K. Mangold, P. Leiderer, and C. Bechinger, Phys. Rev. Lett. 90, 158302 (2003).
[21]
P.H. Dederichs, C. Lehmann, and A. Scholz, Phys. Rev. Lett. 31, 1130 (1973); for a review, see: W. Schilling, J. Nucl. Mater. 69-70, 465 (1978).


File translated from TEX by TTHgold, version 4.00.

Back to Home