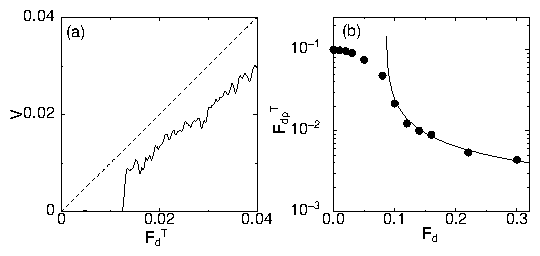 Figure 2:
(a) A series of snapshots of a parallel driven string
as a function of time
with the longitudinal drive in the y-direction and the transverse
drive in the x-direction,
for a system
with Fd = 0.12, just above the transverse depinning threshold.
The transverse depinning occurs via formation of a running kink that
moves
in the direction of the longitudinal drive.
(b) The same snapshots offset in the x direction.
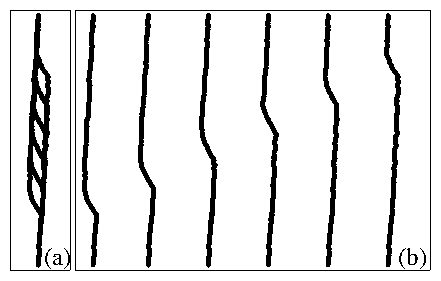
Figure 2:
(a) A series of snapshots of a parallel driven string
as a function of time
with the longitudinal drive in the y-direction and the transverse
drive in the x-direction,
for a system
with Fd = 0.12, just above the transverse depinning threshold.
The transverse depinning occurs via formation of a running kink that
moves
in the direction of the longitudinal drive.
(b) The same snapshots offset in the x direction.
|