Physical Review B 68, 165305 (2003)

Temperature and ac Effects on Charge Transport in Arrays of Metallic Dots

C. Reichhardt and C.J. Olson Reichhardt

Center for Nonlinear Studies and Theoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545

(Received 18 November 2002; published 1 July 2003)

We investigate the effects of finite temperature, dc pulse, and ac drives on the charge transport in metallic arrays using numerical simulations. For finite temperatures there is a finite conduction threshold which decreases linearly with temperature. Additionally we find a quadratic scaling of the current-voltage curves which is independent of temperature for finite thresholds. These results are in excellent agreement with recent experiments on 2D metallic dot arrays. We have also investigated the effects of an ac drive as well as a suddenly applied dc drive. With an ac drive the conduction threshold decreases for fixed frequency and increasing amplitude and saturates for fixed amplitude and increasing frequency. For sudden applied dc drives below threshold we observe a long time power law conduction decay.
I. INTRODUCTION
II. TEMPERATURE EFFECTS
III. TRANSIENT EFFECTS
IV. AC EFFECTS
V. SUMMARY
References

I.  INTRODUCTION

The continuing push toward miniaturization of electronics has led to considerable interest in the conductivity properties of arrays of nanoscale metallic dots. Previous studies of charge transport in arrays of metallic dots have established that there can be a finite voltage threshold for conduction [1,2]. Additionally the current-voltage curves can be nonlinear and exhibit scaling such as that observed for dynamic critical phenomena [3]. Middleton and Wingreen (MW) studied charge transport in 1D and 2D arrays with both simulations and analytic theory [1]. They find scaling in the I-V curves for 1D arrays of the form I = (V/VT − 1)ζ with ζ = 1.0, while for the 2D system they predict ζ = 5/3 and find in simulations ζ = 2.0. Recent simulations by Reichhardt and Olson (RO) [4] also produced similar scaling exponents as well as a crossover from 2D disordered filamentary charge flow regions to more ordered 1D flowing channels for increasing drive. Experimental studies of metal dot arrays have also found scaling in the IV curves for 2D and 1D systems [2,5,6,7,8,9,10,11,12,13]; however, the scaling exponents in these experiments exhibit a wide range of values from ζ = 1.4 to 2.5. The spread in the exponents may be due to different types of disorder present in these arrays.
Recent experiments by Parthasarathy et al. [9] have specifically sought to address the role of different types of array disorder on the current-voltage scaling. They considered varying the global structural order of the array by varying the amount of voids. For structurally ordered systems composed of a triangular monolayer of gold nanocrystals without voids, they observe a single power law scaling with ζ = 2.25 in the current-voltage curves. In this case there is still charge disorder in the substrate and disorder in the inter-particle couplings. For arrays where structural disorder is added, the current-voltage curves could not be fit by a single power law. Simulations by RO for structurally disordered arrays also produced similar behaviors. These results suggest that differences in structural disorder in the earlier experiments may be the cause of the differences in the observed exponents.
Less is known about how other types of disorder, such as thermal disorder, or perturbations, such as ac drives, would affect the scaling or the exponents. Recently Parthasarathy et al. [14] have investigated the role of finite temperature on the current-voltage curves for ordered and structurally disordered gold nanoparticle arrays. They find for the ordered arrays that the threshold voltage decreases linearly with T while the scaling exponent is unaffected. For the disordered arrays the threshold also decreases linearly at low T. Decreases in the threshold with increasing temperature have also been observed in previous experiments on disordered arrays [12,13,15,16,17]. In both the ordered and disordered arrays, for higher temperatures the threshold is lost and the nonlinear scaling of the IV curve disappears and is replaced by linear behavior. Other experiments on ordered arrays have also found that temperature only weakly affects the shape of the IV curves [6,9]. Previous simulations have been limited to T = 0 [1,4] or have considered only very small arrays [17,18].
Another type of perturbation that has recently been considered in experiments on highly resistive samples is the application of a sudden dc drive [19]. The application of a dc voltage that is below the conduction threshold voltage produces a current response that shows a two stage decay. The first stage, shown in Fig. 4 of Ref. [19], is a rapid decay of the current at short time scales that does not fit to a power law. For longer times, however, the current shows a power law decay with I(t) ∝ t−α, with 0.1 < α < 1.0, depending on the applied voltage and temperature.
A third perturbation which can also be applied to the system is an ac drive. To our knowledge, the effect of ac drives on the IV curves has not been investigated by simulation, nor has it been considered in experiments. It is not clear whether increasing ac amplitudes may cause the scaling of the IV curves to be lost, as the perturbation due to temperature did.
In this paper we use the RO model for charge transport through metal dot arrays to consider the effect of finite temperature and ac drives on the threshold behavior and the current-voltage scaling. We also consider the case of sudden applied dc drives and examine the conduction decay. For this work we consider only 2D square arrays, and use system sizes from 20×20 to 60×60. Our results are mainly presented for system sizes of 50×50 which we previously found to be adequately large to capture the essential physics. The sample has periodic boundary conditions in the x and y-directions and contains Nc mobile charges. The equation of motion for a charge i is
fi = ηvi = − Nc
∑
j 
 ∇U(rij) + fp + fdc + fT + fac.
(1)
The mobile charges interact with a Coulomb term, U(r) = q/r. We employ a fast summation technique for computational efficiency to calculate the long-range Coulomb force [20]. The dc driving term is fdc = fdc∧x which would arise from a dc applied voltage V. On each plaquette there is a threshold force fp, chosen from a Gaussian distribution, which prevents the charge from leaving the plaquette until fp is exceeded. This threshold originates from the energy required to add an electron to a dot with charge q. The electron is assumed to tunnel from one dot to the next when the electrostatic energy favors this motion [1]. The threshold for dot j is Vthj = qj/Cj, where Cj is the capacitance of dot j. In experimental systems, this threshold can be altered due to cross-capacitance between neighboring charged dots. In our model, Vth for a given dot is fixed regardless of the charge state of neighboring dots; however, due to the long-range Coulomb interactions between the charges, the effective threshold of the dot is altered by the presence of charges on neighboring dots. We measure the global charge flow or current I = Vx = (1/Nc)∑vi·∧x. Starting from zero we increase the dc drive in increments. When measuring I-V curves, we wait at each increment for 1500 simulation steps before taking data to avoid transient effects. We study transient effects separately in Section II of this paper. To explore finite temperature effects, we add a thermal force term fT which has the properties < fT(t) > = 0 and < fTi(t)fTj(t′) > = 2ηkB T δijδ(t−t′). Here η is a damping constant which we set equal to unity. The damping corresponds to dissipation produced by the motion of the charge. In Section III of this paper, we also add a term representing an external ac drive, fac = Asin(ωt), which would arise from an applied ac voltage. Here A is the amplitude and ω is the frequency of the ac drive.
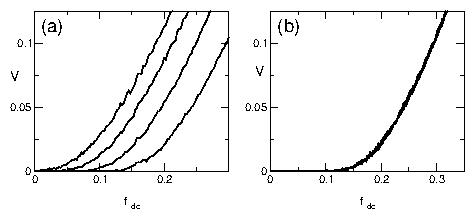
Fig1.png
Figure 1: (a) The velocity V vs dc driving force fdc for (from right to left) T/Tth = 0.0, 0.24, 0.61 and 0.95, where Tth is the temperature at which the threshold disappears, fth=0. (b) The same curves collapsed by applying a linear shift of the x-axis, fshift(T).
Fig2.png
Figure 2: The scaling of the average velocity V vs applied drive for the curves in Fig. 1(b). The dashed line indicates ζ = 2.
Fig3.png
Figure 3: The threshold fth vs T for (circles) the system in Fig. 1 with fp = 4.0 and (squares) a system with fp = 8.0. The solid curves are linear fits. For both sets the temperature axis is normalized by Tth, the temperature at which there is no threshold for the fp = 4.0 system.

II.  TEMPERATURE EFFECTS

We first consider the case of different temperatures and zero ac drive. We normalize our temperature in units of Tth which is the temperature at which the threshold force for motion, fth, becomes zero. In Fig. 1(a) we plot the velocity-force curves (current-voltage curves) for a sample with fp=4.0 for increasing temperature, T/Tth= 0, 0.24, 0.61, and 0.95, indicating that the finite temperature driving threshold fth decreases with temperature. In Fig. 1(b) we show that the curves can be collapsed in the same manner as the experimental curves in Ref. [14], by linearly shifting the x-axis an amount given by fshift(T)=fth(T)−fth(0). This collapse shows that the scaling exponent is independent of temperature. In Fig. 2, a log-log plot of V vs (fdc − fth)/fth for the curves in Fig. 1(b) illustrates a power law scaling with ζ = 2.0 ±0.15, in good agreement with the experimental values [9,14]. In addition, the thresholds are decreasing linearly with temperature, as indicated in Fig. 3. If the temperature is further increased above T/Tth=1, the threshold velocity disappears and the shape of the I-V curve begins to change. Thus above this temperature it is no longer possible to rescale the I-V curves by a simple shift of the x-axis. This is also in agreement with experiment [14].
In Fig. 3 we show the conduction threshold ft vs T for two systems that have different average disorder strength, fp=4.0 and fp=8.0. Both sets are normalized by Tth=1.0, the temperature at which the threshold reaches zero for the fp = 4.0 system (circles). Here the thresholds decrease linearly with temperature for all but the lowest temperatures, T/Tth < 0.1. For the sample with fp = 8.0 (squares), the overall thresholds are higher which is consistent with the increased average force to leave a plaquette. The linear decrease in the threshold is in agreement with experimental observations [14]. We have tested several different methods for determining the threshold, such as using different finite velocity percentages ranging from 0.005 to 0.10, and find consistent linear decreases in the threshold with temperature.
The fact that the scaling of the I-V curves changes with increasing temperature only once a threshold temperature Tth has been exceeded can be understood with a simple physical picture of the channels of charge motion. It was shown previously at T=0 that, for low applied voltages, the charges move through riverlike patterns of channels inside the sample [4]. The exact pattern of the channels in a given sample is determined by the specific realization of disorder within that sample. Throughout the nonlinear segment of the I-V curve, charge motion is confined to a number of channels that increases as fdc is increased. Channels with the lowest barrier to motion open first, followed by channels with increasing barriers to motion. The order in which the channels open is fixed by the disorder realization. When temperature is applied, the barrier to motion in each channel is effectively lowered; however, the relative barrier heights of the channels are unchanged. Thus, at low but finite temperatures, the channels open in the same order as at T=0, but at reduced values of fdc. Therefore the shape of the I-V curve is merely shifted to lower values of fth, but not altered. In contrast, once the temperature is increased enough to completely eliminate the barrier to motion in some of the channels, all of these channels open immediately and the order in which the channels open is changed, which amounts to a change in the topography of the channel structure [21]. This alters the shape of the I-V curve and causes the scaling to be lost, in addition to producing fth=0.
Fig4.png
Figure 4: Images of the charge flow channels at fixed fdc=0.125 and different temperatures. (a) T/Tth=0; (b) T/Tth=0.25; (c) T/Tth=1.0. The total flux of charge through the sample is the same for each image.
To illustrate this picture, in Fig. 4 we show the flow pattern of the charges in our simulation at three different temperatures for fixed fdc=0.125. In Fig. 4(a) and (b), the temperatures T/Tth=0 and T/Tth=0.25 are well below the crossover temperature, and linear scaling of the I-V curves is still possible. Although the details of the smallest channels vary slightly, the overall pattern of the primary channels is the same in both panels. In contrast, Fig. 4(c) shows the channel structure at threshold, T/Tth=1. Here, although there is still inhomogeneous flow, the channel pattern seen at lower temperatures has been destroyed.
If this picture correctly captures the behavior, it implies several experimentally testable features. First, the strength of the disorder will determine the persistence of the channel patterns. In samples with stronger disorder, the threshold temperature should increase, as in Fig. 3. For metallic dots, the disorder strength is determined by the inverse capacitance of each dot, which goes as C=4πϵϵ0 r. Thus, samples containing dots with smaller radii should show a higher threshold temperature. Secondly, the topography of the channels of charge flow is strongly correlated with the noise in the charge velocity, as has been demonstrated for the case of superconducting vortices [21,22]. If the structure of the channels changes above the threshold temperature, this should be observable as a change in the noise characteristics. Finally, in samples that contain voids, the channels are highly constrained by the voids themselves, and the channel pattern cannot be altered even by temperature. Thus, in heavily voided arrays, the linear scaling behavior of the I-V curves should hold to much higher temperatures than in similar void-free arrays.

III.  TRANSIENT EFFECTS

Fig5.png
Figure 5: The velocity vs time for a sudden applied dc drive for the system in Fig. 1 at T = 0.0. From top to bottom, fdc/fth = 0.95, 0.65, and 0.35. The dashed line is a power law with α = 0.45.
Fig6.png
Figure 6: (a) Flow channels for the middle curve in Fig. 5 at fdc/fth=0.65 showing channels moving only for a finite time, then stopping. (b) Flow channels for the top curve in Fig. 5 at fdc/fth=0.95. Here the channels wrap around the periodic boundary conditions and the flow does not come to a stop.
We next consider the case where the dc drive is not slowly increased from zero, but is instead instantly increased to a constant value. Here, transient charge flows are possible when the applied force is stronger than the local threshold for certain regions of the sample, even though the force is below the global threshold of the array. We note that when the drive is slowly increased we do sometimes observe very small charge rearrangements at the onset of a force increment. As in recent experiments [19,23], we measure the transient velocity response V(t) as a function of time. We focus on the T = 0 case for the system with fp=4.0 that was shown in Fig. 1. In Fig. 5 we plot V vs time curves for sudden applied drives of fdc/fth = 0.95, 0.65, and 0.35 that are indicative of the three types of decays we observe. At low drives fdc/fth < 0.5, as illustrated by fdc/fth = 0.35 (bottom), the velocity response drops quickly to zero. In this case, although some charge rearrangement occurs throughout the dots, none of the charges moves more than a lattice constant and there are no correlated riverlike structures of motion. For higher drives such as fdc/fth = 0.65 (middle) we observe two regimes: a short time decay that does not have a power law form, and a slow decay at longer times that fits well to a power law V ∝ tα with α = −0.45 (indicated by the dashed line). For the short time decay we again observe individual charge rearrangements throughout the array which quickly settle down. For the longer times we observe correlated river structures such as those illustrated in Fig. 4(a). The river structures are smaller than the system size and the rivers die out as time passes. In Fig. 6(a) we show the flow patterns for fdc/fth=0.65 (middle curve of Fig. 5) where some 1D winding channels of finite length occur in different places in the sample.
For higher drives, as illustrated by fdc/fth = 0.95 (Fig. 5, top), V saturates to a finite average velocity after an initial decay, even though fdc < fth. Again in this case the initial decay is due to individual charge rearrangements and the long time dynamics corresponds to some channels flowing across the entire array. This saturation occurs due to the finite size of the system. Since we have periodic boundary conditions it is possible for a channel to wrap around the entire system and become stabilized. For smaller systems the saturation occurs at lower fd. in Fig. 6(b) we show the flow channels for the saturation regime where a river flows across the system.
In the experiments [19], the decaying response persisted for more than five orders of magnitude in time. In the simulations we are limited by both the simulation time and by finite size effects. In the power law regime at intermediate drives, the flow occurs in decreasing numbers of channels as previously seen in simulations [4]. In the transient experiments [19] it was speculated that the power law decays may arise due to the Coulomb interactions between dots. We have also considered the case where there is no Coulomb interaction between mobile charges, and find only exponential or stretched exponential decays of the conduction. In addition, the channel structures are not present, indicating that the flow through interacting channels plays an important role in the power law decay of the response.

IV.  AC EFFECTS

Fig7.png
Figure 7: (a) The threshold fth for the system in Fig. 1 normalized by f0, the threshold at zero ac drive, vs ac amplitude for a fixed ac frequency of ω = 0.05. (b) The threshold vs ac frequency for a fixed ac amplitude of A=0.2.
We next consider the case T = 0.0 for the sample that was used in Fig. 1 and measure I-V characteristics for the sample in the presence of a fixed frequency ac drive. In Fig. 7(a) we plot fth/f0 as a function of ac amplitude A for fixed frequency ω = 0.05, where f0 is the threshold for zero ac drive. Here fth monotonically decreases for increasing ac amplitude A, but does not follow a simple functional form. This decrease is reasonable since, during the positive cycle of the ac drive, both the ac and dc drives combine to push the charge over the barrier. We note that f0 = 0.14, indicating that ac amplitudes that are considerably higher than f0, A > f0, still preserve a finite dc threshold force fth. We next fix the ac amplitude to A=0.2 and plot the dependence of fth on the frequency ω in Fig. 7(b). Here, the threshold increases with increasing ac frequency, with fth saturating as 1/ω to f0 at the highest frequencies. At high frequencies, the mobile charge carriers do not have time to respond to the ac drive. We have also measured the scaling of the current-voltage curves, and find that it is independent of both the ac amplitude and frequency. The range of the scaling is, however, reduced by the ac drive.

V.  SUMMARY

In summary, we have investigated transport in 2D metallic dot arrays for finite temperature and ac drives. For zero ac drive and varied temperature, we find a finite temperature conductance threshold which decreases linearly with temperature. Additionally, the I-V curves obey power law scaling with ζ = 2.0, which is independent of the temperature below a threshold temperature. These results are in excellent agreement with recent experiments. For a sudden applied dc drive less than the threshold drive, we find a two stage decay of the velocity response that shows first a fast short time decay that does not fit to a power law. This corresponds to charge rearrangements less than a lattice constant. For longer times there is a slower long time decay that is consistent with a power law where the flow consists of correlated channels that gradually stop. For higher drives that are still below the threshold, some of the channels can move across the entire sample and become stabilized. If the long range Coulomb interaction is removed we observe only a fast exponential decay. We have also studied the effect of superimposing an ac drive on the dc drive and find that, for fixed frequency and increasing ac amplitude, the threshold decreases. Conversely, for fixed amplitude, the threshold decreases for decreasing ac frequency. The scaling of the current-voltage curves is independent of the ac amplitude and frequency; however, the range of the scaling changes.

  ACKNOWLEDGMENTS

We thank H. Jaeger, R. Parthasarathy, and C. Kurdak for useful discussions. This work was supported by the US Department of Energy under Contract No. W-7405-ENG-36.

References

[1]
A.A. Middleton and N.S. Wingreen, Phys. Rev. Lett. 71, 3198 (1993).
[2]
A.J. Rimberg, T.R. Ho, and J. Clarke, Phys. Rev. Lett. 74, 4714 (1995).
[3]
D.S. Fisher, Phys. Rev. B 31, 1396 (1985).
[4]
C. Reichhardt and C.J. Olson Reichhardt, Phys. Rev. Lett. 90, 046802 (2003).
[5]
C.I. Duruöz, R.M. Clarke, C.M. Marcus, and J.S. Harris, Phys. Rev. Lett. 74, 3237 (1995).
[6]
A. Bezryadin, R.M. Westervelt, and M. Tinkham, Appl. Phys. Lett. 74, 2699 (1999).
[7]
C.T. Black, C.B. Murray, R.L. Sandstrom, and S. Sun, Science 290, 1131 (2000).
[8]
C. Kurdak, A.J. Rimberg, T.R. Ho, and J. Clarke, Phys. Rev. B 57, R6842 (1998).
[9]
R. Parthasarathy, X-M. Lin, and H.M. Jaeger, Phys. Rev. Lett. 87, 186807 (2001).
[10]
L. Clarke, M.N. Wybourne, M. Yan, S.X. Cai, L.O. Brown, J. Hutchison, and J.F.W. Keana, J. Vac. Sci. Technol. B 15, 2925 (1997).
[11]
M.N. Wybourne, L. Clarke, M. Yan, S.X. Cai, L.O. Brown, J. Hutchison, and J.F.W. Keana, Jpn. J. Appl. Phys. 36, 7796 (1997).
[12]
C. Lebreton, C. Vieu, A. Pépin, M. Mejias, F. Carcenac, Y. Jin, and H. Launois, Microelectron. Eng. 41-42, 507 (1998).
[13]
M.G. Ancona, W. Kruppa, R.W. Rendell, A.W. Snow, D. Park, and J.B. Boos, Phys. Rev. B 64, 033408 (2001).
[14]
R. Parthasarathy, X-M Lin, K. Elteto, T.F. Rosenbaum, and H.M. Jaeger, cond-mat/0302348.
[15]
L. Clarke, M.N. Wybourne, M. Yan, S.X. Cai, and J.F.W. Keana, Appl. Phys. Lett. 71, 617 (1997).
[16]
A. Pépin, C. Vieu, M. Mejias, Y. Jin, F. Carcenac, J. Gierak, C. David, L. Couraud, and H. Launois, Appl. Phys. Lett. 74, 3047 (1999).
[17]
A.S. Cordan, Y. Leroy, A. Goltzené, A. Pépin, C. Vieu, M. Mejias, and H. Launois, J. Appl. Phys. 87, 345 (2000).
[18]
Y. Leroy, A.S. Cordan, and A. Goltzené, J. Appl. Phys. 90, 953 (2001).
[19]
N.Y. Morgan, C.A. Leatherdale, M. Drndi\'c, M.V. Jarosz, M.A. Kastner, and M. Bawendi, Phys. Rev. B 66, 075339 (2002).
[20]
N. Grønbech-Jensen, G. Hummer, and K.M. Beardmore, Mol. Phys. 92, 941 (1997).
[21]
C.J. Olson, C. Reichhardt, and F. Nori, Phys. Rev. Lett. 80, 2197 (1998).
[22]
C.J. Olson, C. Reichhardt, and F. Nori, Phys. Rev. Lett. 81, 3757 (1998).
[23]
D.S. Ginger and N.C. Greenham, J. Appl. Phys. 87, 1361 (2000).


File translated from TEX by TTHgold, version 4.00.

Back to Home