|Zoltán Toroczkai |  

  
 

Nonlinear Dynamics and Chaos

 
 

Home 

  

Agent-Based Systems

  

Statistical Physics

  

 Nonlinear Dynamics and Chaos

  
 
 

Particle inertia and finite size effects on chaotic advection

The introduction of the realistic inertia and finite particle size effects (buoyancy and Stokes drag) in the equations of motion of a small particle advected by a fluid flow, causes the particle dynamics to be strongly nonlinear even for simple (such as time--periodic) fluid flows, that are not turbulent. Thus, the motion of the advected particles will typically be chaotic.  Here we consider a cellular vortex flow field with periodically varying vorticity as an example for the underlying flow.

 

Time delay function on a (280x280) grid of points, from the first, and the first two cells, respectively.

Picture of the attractor located at infinity in four counter rotating vortex cells. The level curves of the stream function are plotted for reference. 
T. Nishikawa, Z. Toroczkai and  C. Grebogi,  Advective coalescence in chaotic flows, Phys. Rev. Lett. 87, 038301 (2001)
T. Nishikawa, Z. Toroczkai,  C. Grebogi and T. Té, Finite size effects on active chaotic advection,  Phys. Rev. E, 65, 026216 (2002) 
I.J. Benczik, Z. Toroczkai and T. Té, Selective Sensitivity of Open chaotic Flows on Inertial Tracer Advection: Cartching Particles with a Stick, Phys.Rev.Lett. 89, 164501 (2002); cover-page article
I.J. Benczik, Z. Toroczkai and T. Té,  Advection of finite-size particles in open flows, Phys.Rev. E. 67, 036303 (2003); 

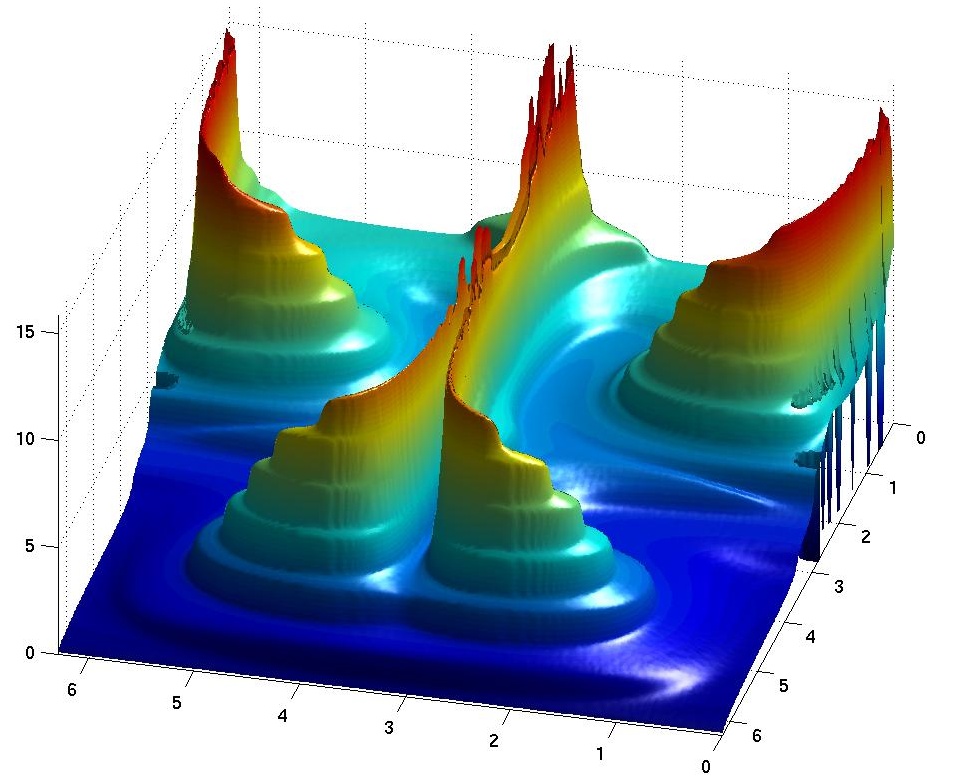
Leapfrogging vortex pairs

The advection problem of passive tracer particles in the time-periodic velocity field of two leaprogging vortex rings (2 vortex pairs) is investigated in the context of chaotic scattering. We numerically determine a few basic unstable periodic orbits of the tracer dynamics, and the non-attracting chaotic set responsible for the motion of particles injected in front of the vortex system. The latter consists of two parts: a hyperbolic component based on strongly unstable periodic orbits, and a non-hyperbolic component that is close to KAM surfaces. The tracer dynamics has a single dimensionless parameter: the energy of the vortex system. As a new phenomenon, we point out the existence of stable bounded trajectories between the vortex pairs at sufficiently large energies. A quantitative characterization of the tracer dynamics in terms of the so-called free energy function is given and the multifractal spectrum of Lyapunov exponents, the escape rate and other characteristics of the transient chaotic motion are determined.

 

  

   

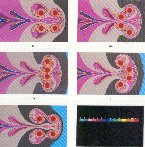
Two leapfrogging vortex rings (in the 2D cross section they appear as two vortex pairs) penetrating a series of differently colored layers. The fractal mixture of colors sits on the unstable manifold of the tracer dynamics.

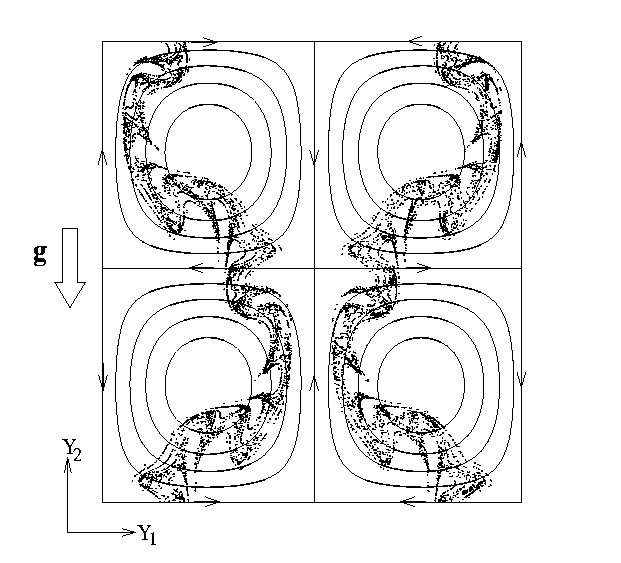
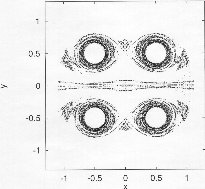
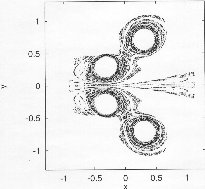
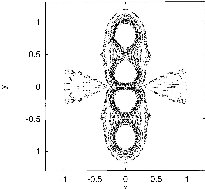
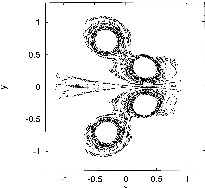
The non-attracting chaotic set of the two leapfrogging vortex pairs at four different instants within one period.
Á. Péntek, T. Té and Z. Toroczkai, Chaotic advection in the velocity field of leapfrogging vortex pairs, J. Phys. A: Math. Gen.  28, 2191 (1995)
Á. Péntek, T. Té and Z. Toroczkai, Fractal tracer patterns in open hydrodynamical flows: the case of leapfrogging vortex pairs, Fractals, 3, 33 (1995)
Á. Péntek, T. Té and Z. Toroczkai, Transient chaotic mixing in open hydrodynamical flows, Int. J. Bif. Chaos  6, 2619 (1996)
 

Fractal basin boundaries: flow past a cylindrical obstacle

We introduce the concept of fractal boundaries in open hydrodynamical flows based on two gedanken experiments carried out with passive tracer particles colored differently. It is shown that the signature for the presence of a chaotic saddle in the advection dynamics is a fractal boundary between regions of different colors. The fractal parts of the boundaries found in the two experiments contain either the stable or the unstable manifold of this chaotic set. We point out that these boundaries coincide with streak lines passing through appropriately chosen points. As an illustrative example, we consider a model of the von Kármán vortex street, a time periodic two-dimensional  flow of a viscous fluid around a cylinder.
 

  
Á. Péntek, Z. Toroczkai, T. Té, C. Grebogi and J. A. Yorke Fractal boundaries in open hydrodynamical flows: Signatures of chaotic saddles, Phys.Rev.E 51, 4076 (1995)
 

A marvel of topological chaos: Wada dye boundaries

Dyes of different colors advected by two-dimensional flows which are asymptotically simple can form a fractal boundary that coincides with a chaotic saddle's unstable manifold. We show that such dye boundaries can have the Wada property: every boundary point of a given color on this fractal set is on the boundary of at least two other colors. The condition for this is the nonempty intersection of the saddle's stable manifold with at least three differently colored domains in the asymptotic inflow region.

  

 
Z. Toroczkai, G. Károlyi, Á. Péntek, T. Té, C. Grebogi and J. A. Yorke Wada dye boundaries in open hydrodynamical flows, Physica A 239, 235 (1997)
  Chaos control

Based on a simple geometrical construction, an algorithm is given for stabilizing hyperbolic periodic orbits of two-dimensional maps, and three-dimensional flows. The method does not require analytical knowledge of the system's dynamics, only a rough location of the linearized region around the periodic orbit to be stabilized (target region). No knowledge is needed about the eigenvalues and eigenvectors of the periodic orbit. In case of flows the perturbative velocity field which controls the system consists of two dissipative memory terms using previous states of the system as feedback. This method can thus be accessible to experiments. A single parameter is needed which is easily measurable from four data points. A novel method to find the target regions is also given.
 

  
Z. Toroczkai, Geometric method for stabilizing unstable periodic orbits, Phys. Lett. A 190, 71 (1994)
B. Sass and Z. Toroczkai, Continuous extension of the geometric control method, J. Phys. A: Math. Gen.  29, 3545 (1996)
 

A chaos control algorithm is developed to actively stabilize unstable periodic orbits of higher-dimensional systems. The method assumes no knowledge of the model equations and a small number of experimentally accessible parameters. General conditions for controllability are discussed. The algorithm is applied to the Hamiltonian problem of point vortices inside a circular cylinder with applications to an experimental plasma system.
 
Á. Péntek, J. B. Kadtke and Z. Toroczkai, Stabilizing chaotic vortex trajectories: an example of high-dimensional control, Phys. Lett. A 224, 85 (1996)
 

Thermodynamic formalism for chaotic maps

Intermittent chaos is investigated by means of an extended version of the statistical-mechanical formalism developed by Sato and Honda [Phys. Rev. A 42, 3233 (1990)]. An exact criterion is given to classify intermittent systems from the point of view of the generated chaotic phases based on the probability distribution of the laminar lengths which is an explicitly measurable quantity from the time series. This criterion provides us with the generalization of the concept of intermittency which broadens the class of critical phenomena associated with the spectrum of dynamical entropies. It is shown that, in contrast to general belief, the presence of the regular chaos phase (i.e., vanishing Rényi entropies for inverse temperatures q > 1) is not necessarily related to intermittency. In fact, the absence of any phase transition or the appearance of an anomalous chaos phase (i.e., infinite Rényi entropies for q < 0) is also possible in intermittent systems. We derive how the pressure, computed from a series of signals of increasing length, approaches its asymptotic value in the regular and anomalous phases.
 

  
Z. Toroczkai and Á. Péntek, Classification criterion for dynamical systems in intermittent chaos, Phys. Rev. E 48, 136 (1993)
Z. Toroczkai and Á. Péntek, Detecting phase transitions in intermittent systems by using the thermodynamical formalism, Z. Naturforsch. 49a, 1235 (1994)
 

Thermodynamics of spin chains via the Ruelle-Araki transfer operator

The Kac model, a spin chain with exponentially decreasing long-range interactions, is investigated by means of a simple functional representation of the transfer operator. An analogy between the thermodynamics of spin chains and of 1D chaotic maps allows us to use techniques developed for generalized Frobenius-Perron equations to extract properties of the spin system, such as free energy and the decay rate of the correlation function. Although the Kac chain does not exhibit a phase transition, we find that the correlation decay shows a nonanalytic behavior at some finite temperature. We are also interested in a generalized version of the Kac model where the interaction still decays exponentially but in an oscillating fashion. This leads to the appearance of complicated patterns in the free energy caused by frustration which is a typical effect for disordered systems. By working out the analogy with 1D chaotic maps in more detail, we show how one can construct maps with the same thermodynamics as the spin chain. The associated maps turn out to be not smoothly differentiable, and their derivatives exhibit fractal properties.
 

  
Á. Péntek, Z. Toroczkai, D.H. Mayer, and T. Té, Kac Model from a dynamical system's point of view, Phys. Rev. E 49, 2026 (1994)
Á. Péntek, Z. Toroczkai, D.H. Mayer, and T. Té, A generalized Kac model as a dynamical system,  Z. Naturforsch. 49a,  1212 (1994)