
Back to MAIN PAGE
Page under Construction!
We study the asymptotic scaling properties of a massively parallel algorithm for discrete-event simulations where the discrete events are Poisson arrivals. The evolution of the simulated time horizon is analogous to a non-equilibrium surface. Monte Carlo simulations and a coarse-grained approximation indicate that the macroscopic landscape in the steady state is governed by the Edwards-Wilkinson Hamiltonian. Since the efficiency of the algorithm corresponds to the density of local minima in the associated surface, our results imply that the algorithm is asymptotically scalable. The figure below presents the density plots for the nearest-neighbor two-slope distribution. (a) L=10000. (b) L=3, exact.

The aim of statistical mechanics is to relate the macroscopic observables to the microscopic properties of the system. Before performing any such derivation one always has to specify the spectrum of length-scales the analysis will comprise: while 'macroscopic' is usually defined in a unique way by the every-day-life length scale, the 'microscopic' is never so obvious, and the choice of the best lower-end scale is highly non-universal, it is system dependent, usually left to our physical 'intuition', or it is set by the limitations of the experimental instrumentation. It is obvious that in order to derive the laws of the gaseous matter we do not need to use the physics of quarks, it is enough to start from an effective microscopic model (or Hamiltonian) on the level of molecular interactions. Once a lower lenght scale is set on which we can define an effective microscopic dynamics, it becomes meaningful to ask questions about local properties at this length scale, e.g. nearest neighbor correlations, extremal-point densities, etc.. These quantities are obviously not universal, however their behavior against the variation of the length scales can present qualitative and universal features. Here we study the dynamics of macroscopically rough surfaces via investigating an intriguing miscroscopic quantity: the density of extrema (minima) and its finite size effects. We derive a large number of exact analytical results about these quantities for a large class of non-equilibrium surface fluctuations described by both pure relaxational processes and linear Langevin equations, and solid-on-solid (SOS) lattice-growth models. Via an analogy between a simple SOS lattice-growth model and the time horizon of conservative parallel algorithms these results allow us to prove the asymptotic scalability of parallel computing when using such algorithms, i.e., the fact that the efficiency of such a computation does not vanish with increasing the number of processing elements, but it has a lower non-trivial bound.
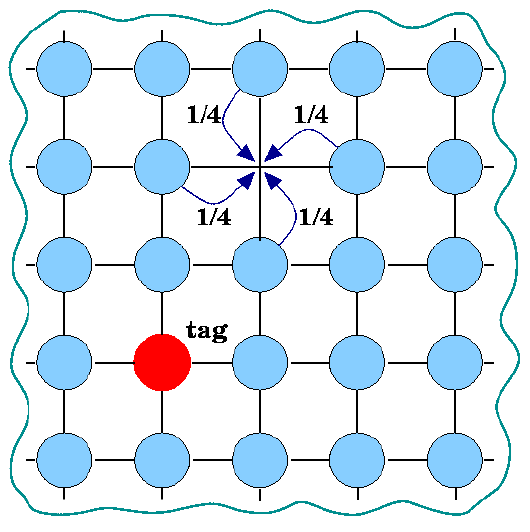
We analyze the lattice walk performed by a tagged member (the red disk in the figure below) of an infinite 'sea' of particles (the light blue disks) filling a d-dimensional lattice, in the presence of a single vacancy (the empty node). The vacancy is allowed to be occupied with probability 1/2d by any of its 2d nearest neighbors, so that it executs a Brownian walk. The only interaction between the particles is hard core exclusion, and particle-particle exchange is forbidden. Thus, the tagged particle, differing from the others only by its tag, moves only when it exchanges places with the hole. In this sense, it is a random walk 'driven' by the Brownian vacancy. The probability distributions for its displacement and for the number of steps taken, after n-steps of the vacancy, are derived. Neither is a Gaussian! We also show that the only nontrivial dimension where the walk is recurrent is in d=2. As an application, we compute the expected energy shift caused by a Brownian vacancy in a model for an extreme anisotropic binary alloy. Our studies also include a Monte-Carlo study and a mean-field analysis for interface erosion caused by mobile vacancies.
We study a random walk on a one-dimensional periodic lattice with arbitrary hopping rates. Further, the lattice contains a single mobile, directional impurity (defect bond), across which the rate is fixed at another arbitrary value. Due to the defect, translational invariance is broken, even if all other rates are identical. The structure of Master equations lead naturally to the introduction of a new entity, associated with the walker-impurity pair which we coin as 'quasi-walker'. Analytic solution for the distributions in the steady state limit is obtained. The velocities and diffusion constants for both the random walker and impurity are given, being simply related to that of the quasi-particle through physically meaningful equations. As an application, we extend the Duke-Rubinstein reptation model of gel electrophoresis (figure below) to include polymers with impurities (neutral monomers represented as open circles) and give the exact distribution of the steady state.
Persistence exponents are notoriously hard to calculate even for simple processes such as the deterministic diffusion equation with random initial condition. As a matter of fact in spite of the extensive work and the large number of publications since 1996, a rigorous derivation of the exponent is still missing.
We present a new method for extracting the persistence exponent theta for the diffusion equation, based on the distribution P of 'sign-times'. With the aid of a numerically verified Ansatz for P we derive an exact formula for theta in arbitrary spatial dimension d. Our results are in excellent agreement with previous numerical studies. Furthermore, our results indicate a qualitative change in P above d ~ 36, signalling the existence of a sharp change in the ergodic properties of the diffusion field.
A soldier receives the order to mine a field with mines that have delayed activation. Once a mine is planted it will not go off when stepped on it, for a finite time interval L, which is called the activation time, or delay time. After the activation time has elapsed, the mine becomes active and will blow if touched. Thus our soldier can step without worries on a mine that has been planted not earlier than L. Unfortunately, the soldier become very drunk for the day he had to plant the mines. He could barely wander from planting site to planting site and he could neither remember which planted mines became active nor where he even planted them. The soldier became a simple random walker on the field. Naturally the following question arises: - what is the probability that our soldier is able to plant N mines without being blown to the skies? In more mathematical terms this problem amounts to the determination of the statistics of simple random walk paths of length N that do not contain loops longer than L. Obviously the L=0 case corresponds to the pure self-avoiding walk, and the L = N case represents the simple random walk without any constraints.
In one dimension the pure self-avoiding walk has a trivial solution: one straight path to the left and another straight path to the right. The problem of the delayed self-avoiding walk in one dimension is still awaiting for a rigorous solution for general L !
Intermittent chaos is investigated by means of an extended version of the statistical-mechanical formalism developed by Sato and Honda [Phys. Rev. A 42, 3233 (1990)]. An exact criterion is given to classify intermittent systems from the point of view of the generated chaotic phases based on the probability distribution of the laminar lengths which is an explicitely measurable quantity from the time series. This criterion provides us with the generalization of the concept of intermittency which broadens the class of critical phenomena associated with the spectrum of dynamical entropies. It is shown that, in contrast to general belief, the presence of the regular chaos phase (i.e., vanishing Rényi entropies for inverse temperatures q > 1) is not necessarily related to intermittency. In fact, the absence of any phase transition or the appearance of an anomalous chaos phase (i.e., infinite Rényi entropies for q < 0) is also possible in intermittent systems. We derive how the pressure, computed from a series of signals of increasing length, approaches its asymptotic value in the regular and anomalous phases.
The Kac model, a spin chain with exponentially decreasing long-range interactions, is investigated by means of a simple functional representation of the transfer operator. An analogy between the thermodynamics of spin chains and of 1D chaotic maps allows us to use techniques developed for generalized Frobenius-Perron equations to extract properties of the spin system, such as free energy and the decay rate of the correlation function. Although the Kac chain does not exhibit a phase transition, we find that the correlation decay shows a nonanalytic behavior at some finite temperature. We are also interested in a generalized version of the Kac model where the interaction still decays exponentially but in an oscillating fashion. This leads to the appearance of complicated patterns in the free energy caused by frustration which is a typical effect for disordered systems. By working out the analogy with 1D chaotic maps in more detail, we show how one can construct maps with the same thermodynamics as the spin chain. The associated maps turn out to be not smoothly differentiable, and their derivatives exhibit fractal properties.
Back to MAIN PAGE