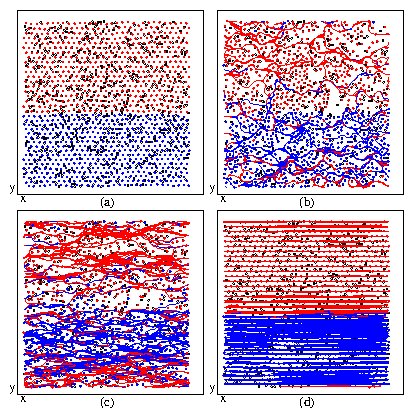
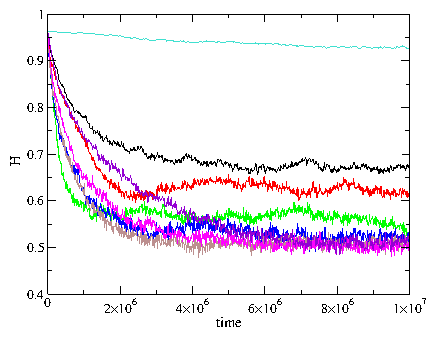
 Figure 2: Measure of local homogeneity H vs time for the system
in Fig. 1 at Fd=
0.05 (black), 0.1 (red), 0.25 (green), 0.4 (blue),
0.5 (brown), 0.6 (magenta), 0.7 (violet), and 1.1 (top curve).
H = 1 for phase segregation and H = 0.5 for complete mixing.
Figure 2: Measure of local homogeneity H vs time for the system
in Fig. 1 at Fd=
0.05 (black), 0.1 (red), 0.25 (green), 0.4 (blue),
0.5 (brown), 0.6 (magenta), 0.7 (violet), and 1.1 (top curve).
H = 1 for phase segregation and H = 0.5 for complete mixing.
|