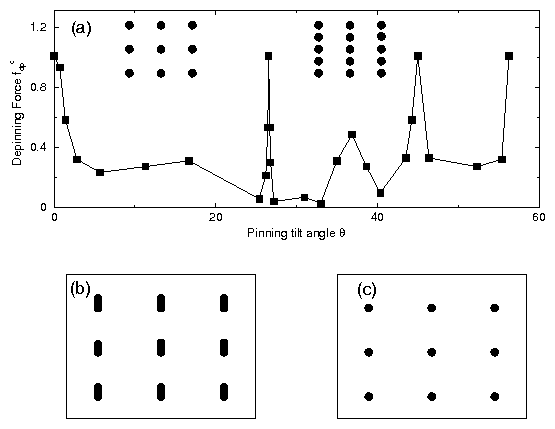
 Figure 1: The critical depinning force fdpc versus the tilt angle
θ of the pinning sites. The vortex arrangements as seen from the
z-direction are outlined for different tilt angles θ = 0 left and
θ = 26.6 right.
(b) shows the pinned vortex arrangement for θ = 1.5° where
the vortices stay aligned with the pins. (c) shows the moving vortex
state for θ = 1.5°
where the vortices have realigned with the z direction.
Figure 1: The critical depinning force fdpc versus the tilt angle
θ of the pinning sites. The vortex arrangements as seen from the
z-direction are outlined for different tilt angles θ = 0 left and
θ = 26.6 right.
(b) shows the pinned vortex arrangement for θ = 1.5° where
the vortices stay aligned with the pins. (c) shows the moving vortex
state for θ = 1.5°
where the vortices have realigned with the z direction.
|
