Research Interests
I study amorphous materials under shear, which involves many problems at the intersection of physics, geophysics, and materials science. A summary of some of my research projects are given below. For more detailed information on my research, see the publications page.
Stick Slip Instabilities with Shear Bands
Strain Localization in Dynamic Rupture Simulations
Dynamic Earthquake Ruptures with STZ Theory
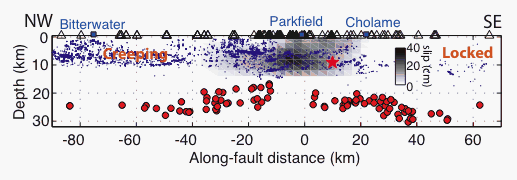
Earthquakes tend to occur in the upper 15 km of the crust, where rock deformation occurs in a brittle manner. Below 15 km depth, the fricitonal properties gradually transition to a ductile mode of deformation. Recent improvements in seismic and GPS networks have revealed that deformation below 15 km depth can occur in a transient manner, exhibiting phenomena ranging from tremor (tiny earthquakes repeatedly occuring at large depths) to silent slip events that release large amounts of strain but radiate little seismic energy. These events provide insight into the mechanisms of deformation, and can help constrain models. Here, we utilize the observations of such events, coupled with a simple model for brittle and ductile friction, to constrain the frictional properties in the lower part of the crust.
 |
| Figure: The San Andreas Fault at Parkfield. Earthquakes are shown with blue dots, and occur in the upper 15 km of the crust. At larger depths, tremor events occur, and event locations are shown by the larger red dots. (Adapted from Shelly and Hardebeck, Geophysical Research Letters, 2010). |
We develop a simple frictional model for tremor, combining brittle and ductile components. The brittle components are frictional elements that resist motion and fail by breaking suddenly, representing fault patches that are brittle and fail, and the ductile component is a rate strengthening damping. With an appropriate combination of brittle and ductile frictional strengths, the model produces events like tremor bursts.
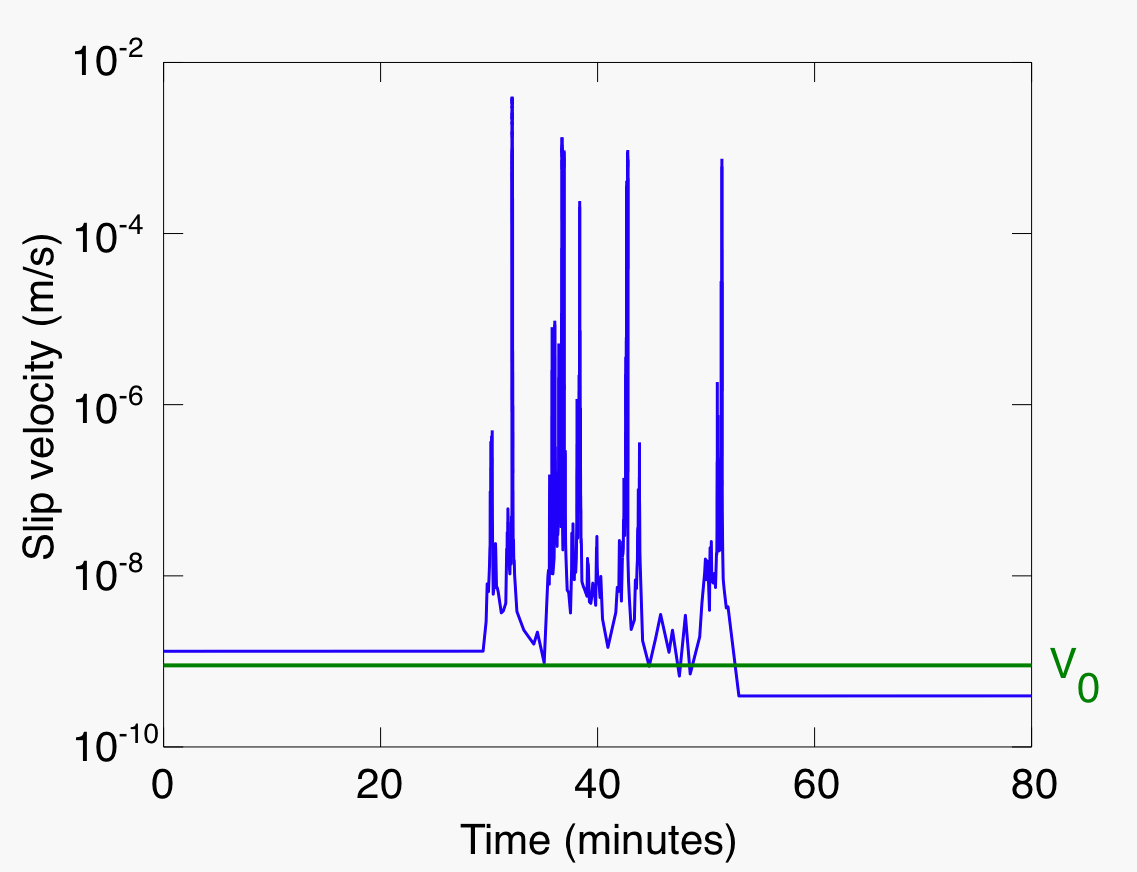 |
| Figure: Model dynamics for a tremor event. The model fails by producing several individual failure events closely spaced in time, similar to observations of tremor in many tectonic regimes. |
Additionally, we can map out the different types of slip behaviors that the model produces as a function of brittle and ductile strengths. The model produces all observed slip behaviors, including earthquakes, tremor, silent transient slip, and steady sliding.
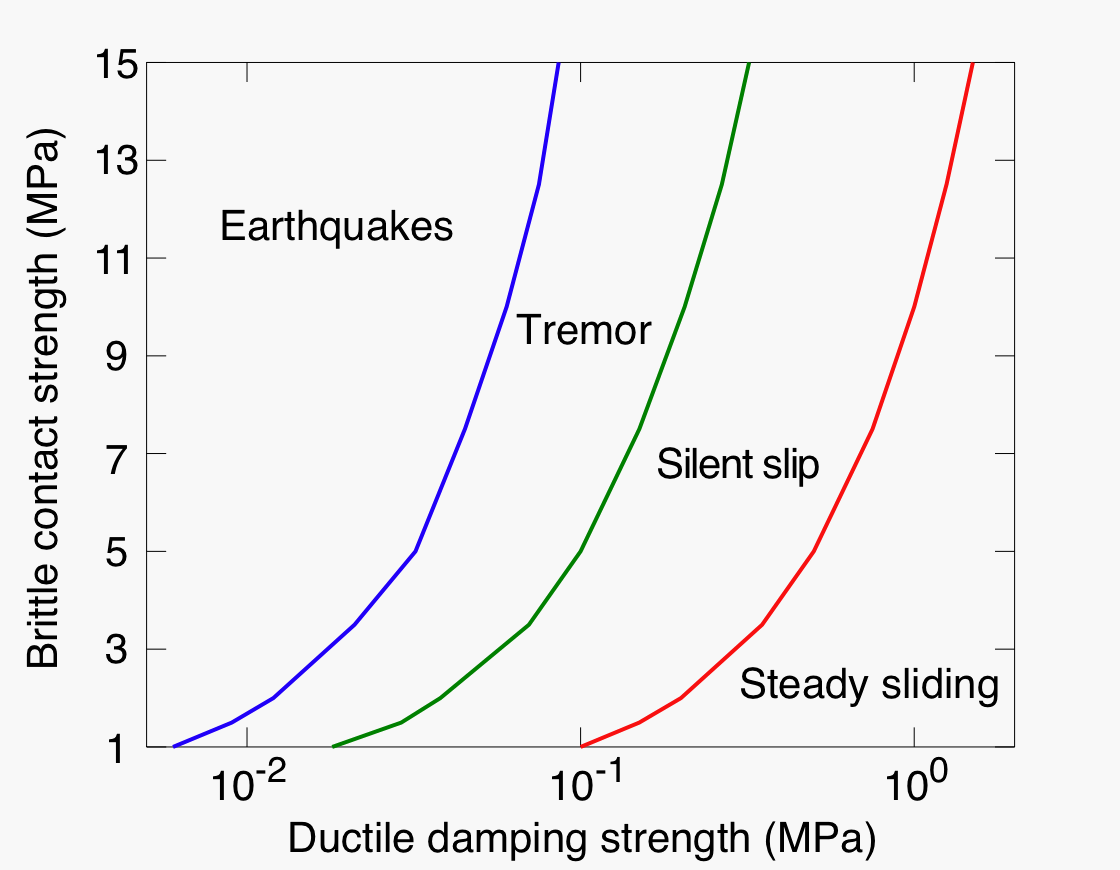 |
| Figure: Phase diagram for tremor, showing the slip behavior that occurs as a function of the brittle and ductile strengths in the model. |
More about modeling tectonic tremor can be found here.
Most experimental studies of friction focus on the macroscopic dynamics that can be measured in the laboratory, while theoretical studies look at microscopic mechanisms for deformation. A challenge is to connect the microscopic dynamics to the larger scale friction. We attack this problem using a constitutive model based on STZ Theory that resolves the microscopic localization of strain, while remaining tractable to study friction at larger length and time scales. Here, we focus on a simple spring slider model and study the transition between stick-slip and steady sliding. Stick-slip occurs when steady frictional sliding is unstable and the block sticks and then fails rapidly, rather than sliding with a steady frictional resistance.
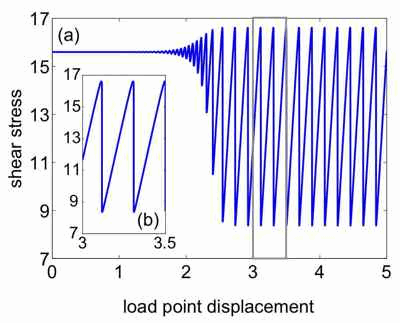 |
| Figure: Plot of shear stress as a function of load point displacement (displacement of the end of the spring driven at constant velocity) during stick-slip. The inset shows that the slider motion is not oscillatory, and that the block sticks as the shear stress increases linearly and then fails rapidly when the shear stress drops. |
We perform a linear stability analysis with the STZ Equations, and make quantitiative predictions for the effect of strain localization on when frictional sliding transitions from steady sliding to stick-slip. The transition can be studied as a function of the stiffness of the spring pulling the block, and the speed at which the block is driven. Strain localization leads to stick-slip over a larger range of parameters than the case without a shear band, and our analysis makes a quantitative prediction as to the effect of the shear band width on the stiffness and driving rates where stick-slip occurs.
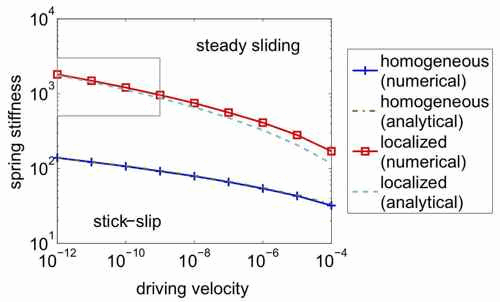 |
| Figure: Phase diagram for slider motion as a function of spring stiffness and driving velocity. Above each curve, the block slides stably, and below stick-slip occurs. Our analytical predictions agree very well with results from numerical integration of the STZ equations. The upper curve is for strain localization, which shows that localization leads to stick-slip for a larger range of parameters. |
Additionally, we find that strain localization produces irregular stick-slip cycles. At low driving rates and low spring stiffnesses, stick-slip with strain localization occurs with irregular recurrence times. This provides a physical mechanism for exotic friciton dynamics, and connects microscopic failure mechanisms to macroscopic dynamics.
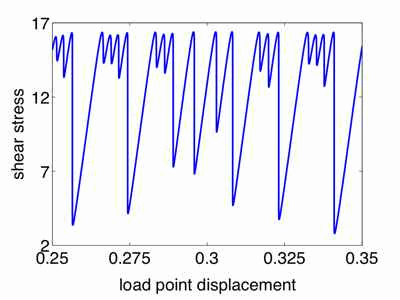 |
| Figure: Irregular stick-slip with STZ Theory. Plot shows shear stress as a function of load point displacement. Groups of events usually include several small events followed by a large event, but successive larger events are also possible. |
More about stick-slip with strain localization can be found here.
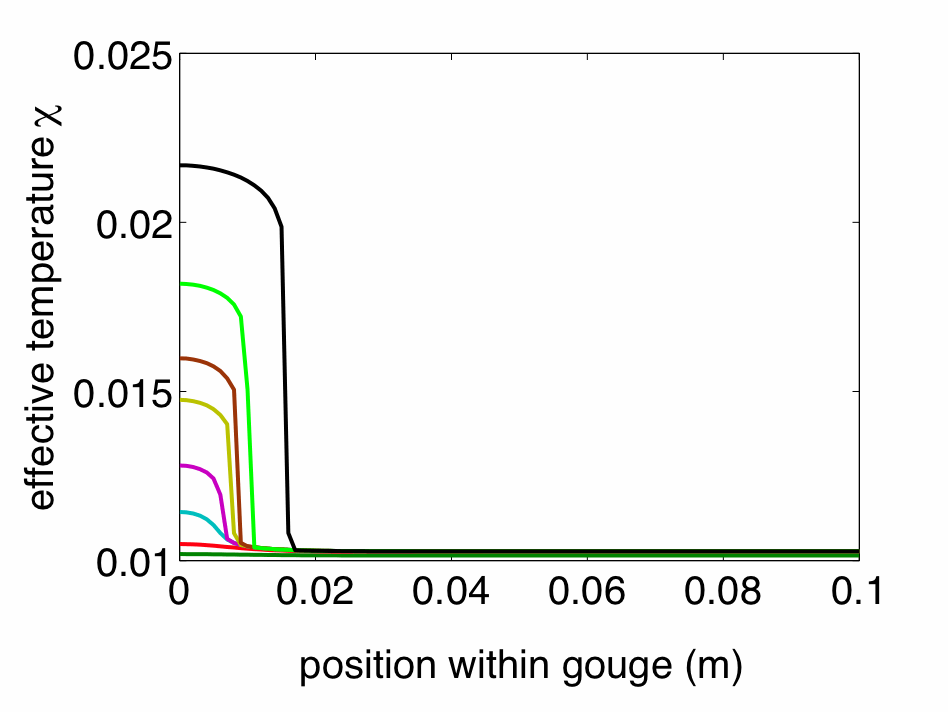 |
| Figure: Plot of effective temperature evolution during a dynamic rupture simulation. The shear band spontaneously forms at the left of the plot, and grows as the fault slips. |
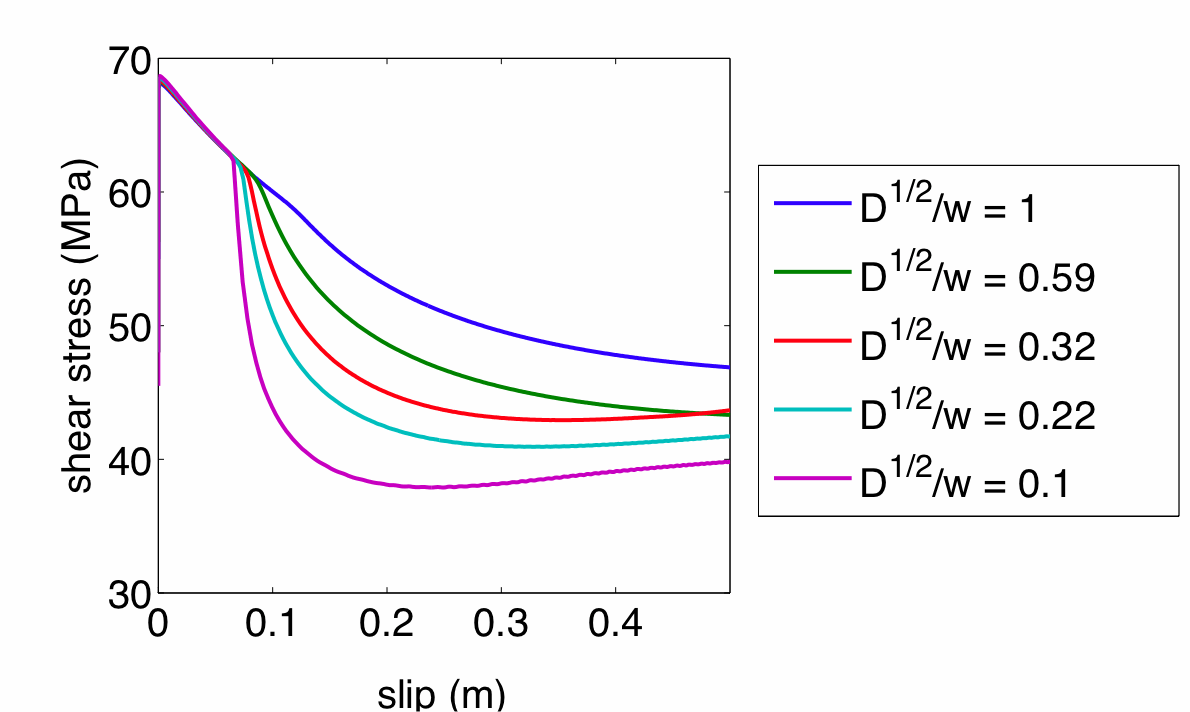 |
| Figure: Plot of shear stress as a function of slip for a variety of different diffusion length scales. As the diffusion length scale is increased, the shear band is narrower and we see additional dynamic weakening during fault slip. |
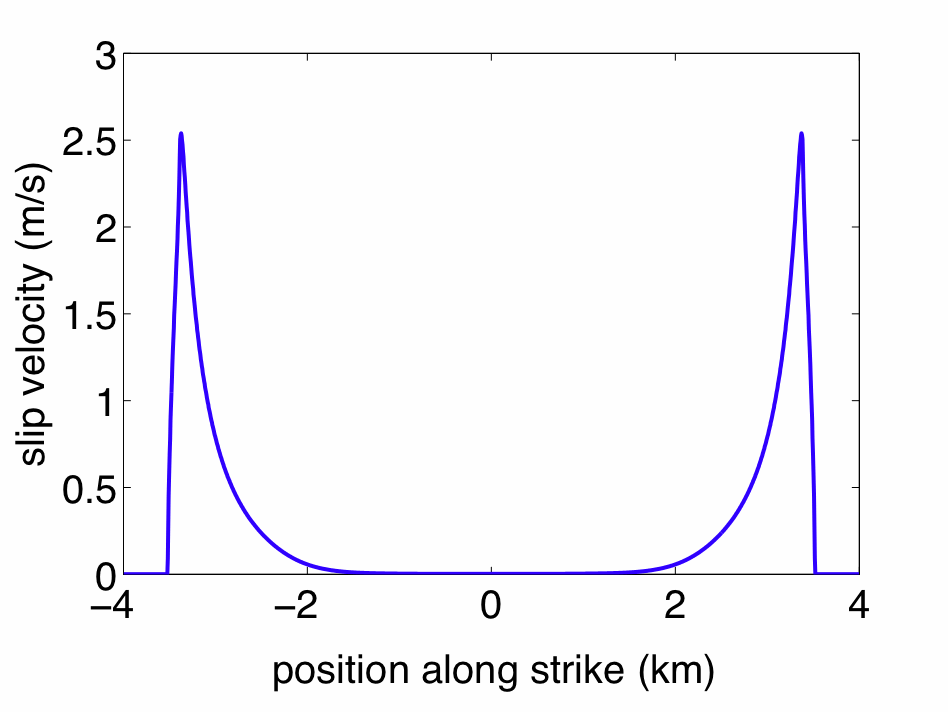 |
| Figure: A pulse-like rupture with dynamic formation of a shear band. The dynamic weakening due to localization allows for rupture to propagate as a self-healing pulse at low shear stress. |
Our results illustrate that small scale processes such as strain localization can have effects that are relevant at the larger scale of faults, and that accurately capturing the strain profile in the gouge is an important consideration in modeling earthquake rupture.
More details on strain localization in earthquake ruptures can be found here and here.
 |
| Figure: Plot comparing the FV Law (right) with laboratory data for the frictional length scale for a layer of gouge (left). |
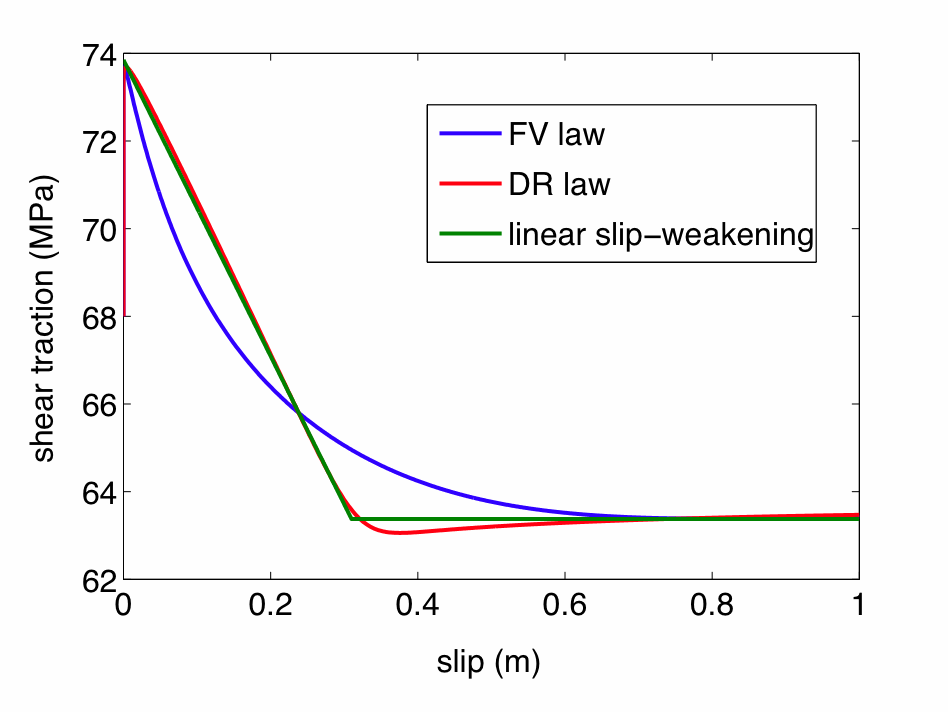 |
| Figure: Plot showing shear traction as a function of slip. The SW and DR laws exhibit similar behavior, but the FV law weakens in a distinct manner with slip. The FV law is different due to the slip rate dependence of the frictional length scale. |
We also look at the DR and FV laws modified to allow for more rapid weakening with slip velocity. Friction laws with rapid weakening allow for rupture as a self-healing slip pulse. Pulse-like ruptures can propagate on faults with significantly lower shear stress.
 |
| Figure: Pulse-like rupture with the FV law with rapid weakening. Each point on the fault slips for a short period of time relative to the duration of the earthquake. Slip rates are larger, and the shear stress is lower. |
More details on earthquake rupture with STZ Theory can be found here.