Barros' Research

Current Projects

Scale bridging from atomistic to mesoscale fluid dynamics

Fluid simulations at the largest (continuum) scales are well described by standard equations, such as Navier Stokes. However, there is a region of intermediate (meso) scales for which (a) atomic level physics plays an important role, but (b) full atomistic resolution is too expensive.

In this project, we are investigating ways to automatically develop mesoscale models of fluid dynamics (such as generalizations of the lattice Boltzmann method) using data from large-scale atomistic simulation (i.e., molecular dynamics).

In collaboration with Tim Germann (PI) and many others.

Active learning for quantum chemistry and materials

Outsmarting quantum chemistry through active learning Nature Commun., to appear [ChemRxiv:6744440].

Molecular dynamics simulation has wide-ranging applications in fields such as materials science, chemistry, molecular biology, and physics. For each atomic configuration, the potential energy and forces follow from the quantum mechanics of electrons. The full Schrödinger equation is extremely difficult to solve, and in practice some level of approximation is necessary. A common choice is Density Functional Theory (DFT) which scales like $\mathcal O(N^3)$ in the number of atoms $N$. Going to higher levels of accuracy becomes dramatically more expensive. Such methods are essentially intractable for large-scale dynamical simulations, in which the atomic forces must be calculated at each integration time-step.

Machine learning potential energy surfaces are poised to achieve nearly full quantum accuracy, but at a much reduced computational cost. Many modeling approaches are possible; our team has developed HIP-NN and ANI neural networks. We have come to believe that the most pressing need for better ML models is to improve the quality and diversity of the training data. Fortunately, we are in a position to generate better datasets ourselves by intelligently performing thousands to millions of quantum calculations.

We are developing active learning methodologies to collect new data (from quantum calculations) whenever we can identify that the ML model is unable to make a good prediction. There are two challenges to address: (1) How can we rapidly find new atomic configurations that are potentially physically relevant, and (2) How can we quantify the uncertainty of the ML predictions?

Preliminary work by our team and others indicates that the active learning approach can yield highly effective and general ML models of potential energies. But we believe there is still much room for fundamental advances in the active learning methodologies.

In collaboration with Sergei Tretiak, Justin Smith, Ben Nebgen, Nick Lubbers, and many others.

Machine learning for earthquake physics

Machine Learning Predicts Laboratory Earthquakes, Geophys. Res. Lett. [arXiv:1702.05774] (top 10 most downloaded paper in 2017).
Picked up by Scientific American, Technology Review, and phys.org.

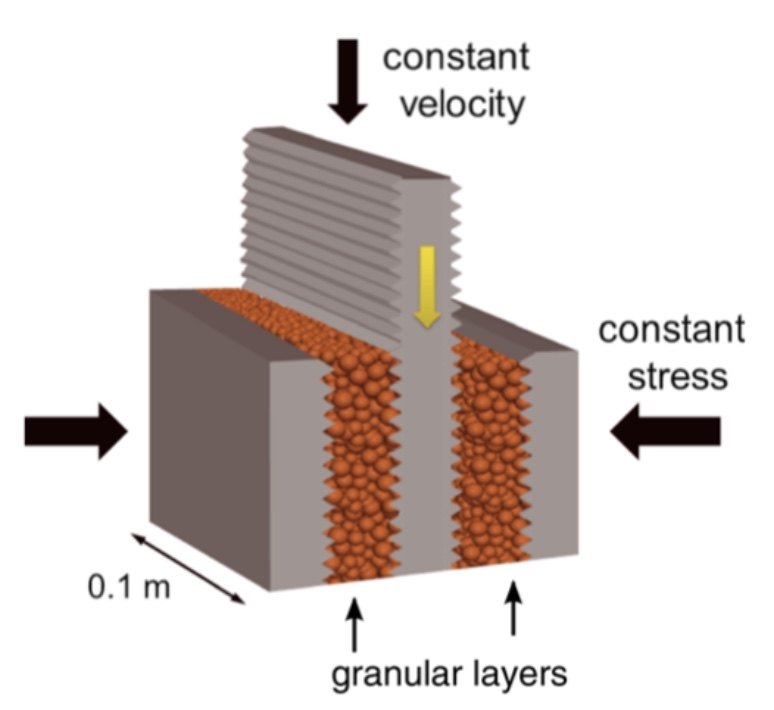Earthquakes cause tremendous destruction. A better understanding of the underlying geophysical processes may eventually lead to early warning systems with the potential to save lives. Some fault systems are much easier to understand than others. In our bottom-up approach we first seek to understand lab-quakes, i.e. quakes produced in a laboratory experiment, pictured to the left. A slider plate is pushed downwards and must overcome friction transmitted through granular layers.

The stress on the slider plate loads up steadily and then drops abruptly at the lab-quake event. This cycle may repeat hundreds of times, producing an ideal dataset for machine learning. Whereas previous attempts at earthquake prediction focused on learning from smaller catalogued events, here we use all data available from the acoustic strain signal.

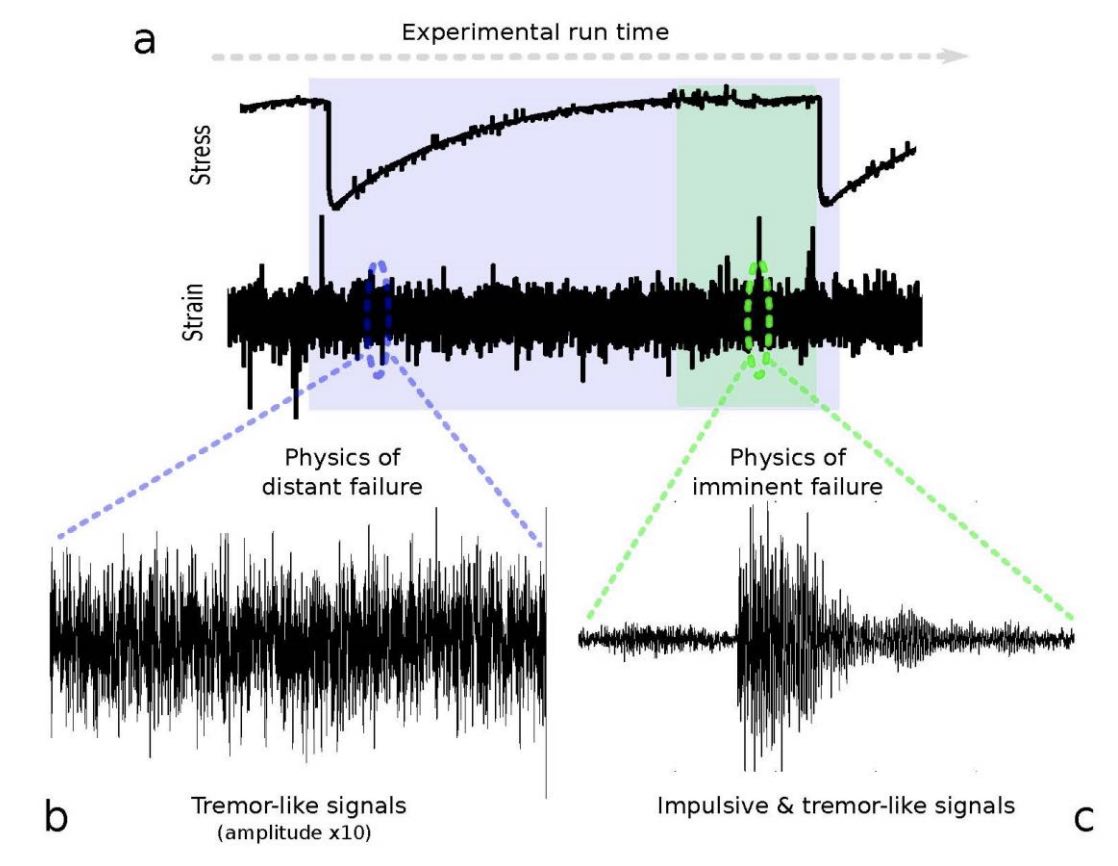(a) We train a machine learning model to predict the time until the next big lab-quake using a local time window of the strain waveform. (b) The machine learned model makes surprisingly accurate predictions long before failure. The most important feature is the signal variance, which had previously been interpreted as noise. (c) Closer to the failure event, precursor events are easier to identify.

There are strong indications that these machine learning techniques are also effective for certain types of real earthquake fault systems.

In collaboration with Paul Johnson (PI), Bertrand Rouet-Leduc, Claudia Hulbert, Nick Lubbers, and many others.

Numerical methods for linear scaling quantum dynamics

Efficient Langevin simulation of coupled classical fields and fermions, Phys. Rev. B [arXiv:1303.1101].
Semiclassical dynamics of spin density waves, Phys. Rev. B (Editors' Suggestion) [arXiv:1708.08050].
Gradient-based stochastic estimation of the density matrix, J. Chem. Phys. (Editor's Pick) [arXiv:1711.10570].

We consider problems in which effectively classical degrees evolve according to interactions that are mediated by quantum mechanics. For example, in quantum (Born-Oppenheimer) molecular dynamics, the positions of atomic nuclei are held fixed while solving the quantum mechanics of electrons. The full many-body problem is hard, but many approximation techniques are available. Commonly, one requires a fast subroutine to diagonalize an evolving single-particle Hamiltonian $H_{ij}$, i.e., to solve a quadratic Hamiltonian in the fermions, $$\mathcal H = c^\dagger_i H_{ij} c_j.$$ Specifically, one may require fast linear-scaling methods to estimate the density matrix, $$\langle c^\dagger_i c_j \rangle = f(H)_{ij} = \left( \frac{1}{1+e^{\beta H}} \right)_{ij}.$$ For insulators, $f(H)_{ij}$ decays quickly with the distance between sites $i$ and $j$. For metals, polynomial decay makes the task more challenging. The Fermi function, $f(x)$, can be expanded in, e.g., Chebyshev polynomials $T_m(x) = \cos (m \arccos x)$. If we further apply a probing approximation, $f(H) \approx f(H) R R^\dagger$, we can achieve a linear scaling numerical method using the sparsity of $H_{ij}$. But how good is this approximation for a given $N \times S$ random matrix $R$? If the matrix elements $R_{ij}$ are uncorrelated, the error in $R R^\dagger \approx I$ is unbiased and scales like $1 / \sqrt{S}$. It's possible to do better by designing the matrix $R$ to take advantage of the polynomial (or faster) decay of $f(H)_{ij}$. With our latest techniques the stochastic error in approximating $f(H)$ scales like $S^{-1/d} / \sqrt{S}$ in spatial dimension $d$ for metals at zero temperature.

Another research topic is to go beyond the Born Oppenheimer approximation. For example, in the spin-density wave dynamics shown above (colored by scalar chirality), we may wish to capture the quantum fluctuations of the local magnetic moments. We are exploring various approaches that balance numerical expedience (avoiding or limiting the fermion sign-problem) and accuracy.

In collaboration with Cristian Batista, Zhentao Wang, and Hidemaro Suwa.

Previous Projects

Neural network architectures for quantum chemistry

Hierarchical modeling of molecular energies using a deep neural network, J. Chem. Phys. [arXiv:1710.00017].

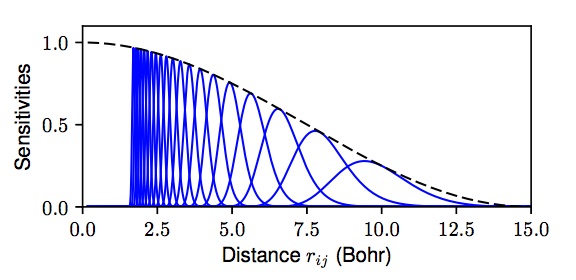
There is tremendous interest in using machine learning (ML) to automatically construct potential energy surfaces from large datasets of quantum calculations. Here we build upon recent advances in computer vision, e.g., using the principles of deep convolutional neural networks (ConvNets) for translation-insensitive processing of an image plane. Because atoms live off-lattice, the traditional ConvNet architecture needs to be suitably generalized. An atomic configuration can be represented generally as a graph, with the edge weights containing distance information between atoms. In this representation, convolutional filters generalize to sensitivity functions that pass information between atoms. This approach has found great success in, e.g., DTNN, MPNN, and SchNet models, which achieve chemical-level accuracy at linear scaling cost in system size $N$.

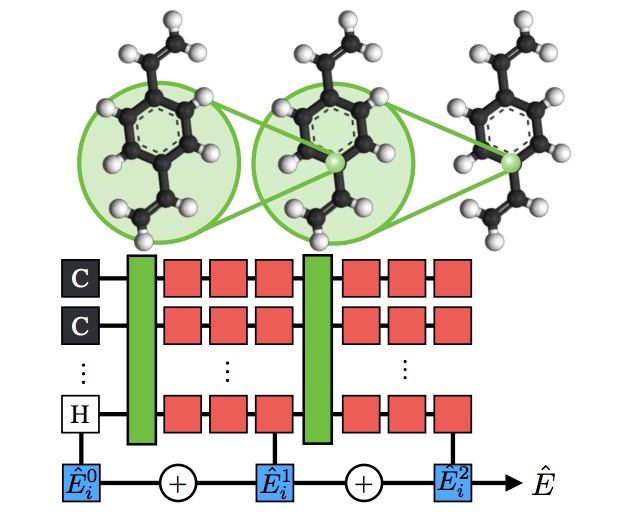
We are working to develop new ML architectures that naturally encode even more physical knowledge. For example, in our Hierarchically Interacting Particle Neural Network (HIP-NN), pictured above, multiple hierarchical layers contribute to the model's total energy prediction. This network structure has the flavor of a physical Many Body Expansion, and achieves record-breaking performance on multiple benchmarks. Further progress in ML architectures is especially important in light of the quantum chemistry community's migration toward higher-fidelity datasets; as each quantum calculation becomes vastly more expensive, the dataset sizes are becoming much smaller, and ML must do more with less.

In collaboration with Nick Lubbers and Justin Smith.

Kinetics of liquid-to-solid transformations

Liquid to solid nucleation via onion structure droplets, J. Chem. Phys. [arXiv:1308.5244].
Phase transition kinetics in systems with long-range interactions (Chapter 3.3), PhD thesis [PDF].

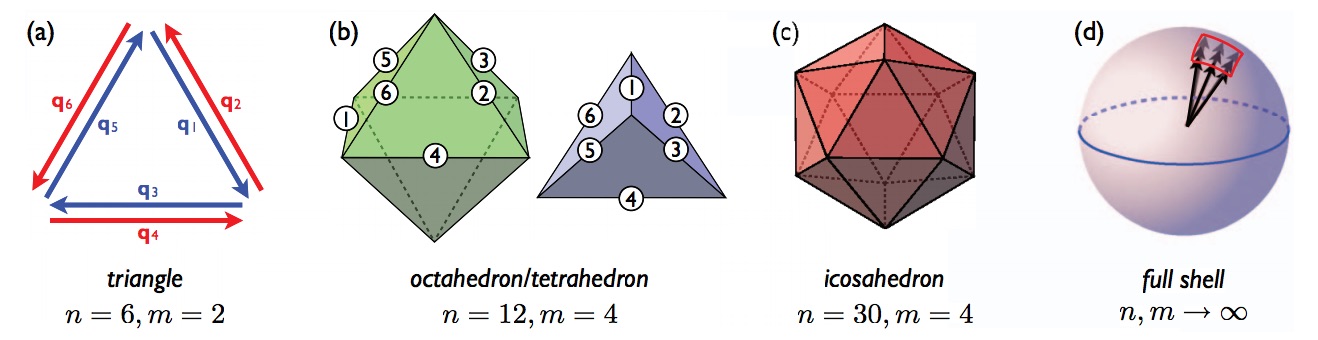
One of the topics in my PhD work was the dynamics of liquid-to-solid phase transformations. The transformation is initiated by the formation of a nucleating droplet, i.e., a rare fluctuation in the metastable liquid phase that leads to unstable growth. In the classical theory of nucleation, the most likely droplet will be a localized "bubble" of the stable solid phase embedded within the metastable liquid. However, for deeper quenches, the nucleating droplet can have a strikingly different symmetry than that of the stable crystal. We studied a model system for which analytical calculations are tractable (consistent with prior work by Alexander-McTague and others). After what has been called a "tour de force" calculation, we found that the optimal nucleating droplet (i.e., the saddle point configuration with lowest free energy barrier) has a highly unexpected onion structure, with reciprocal wavevectors pointing everywhere in the "full shell" pictured above.

In collaboration with Bill Klein.