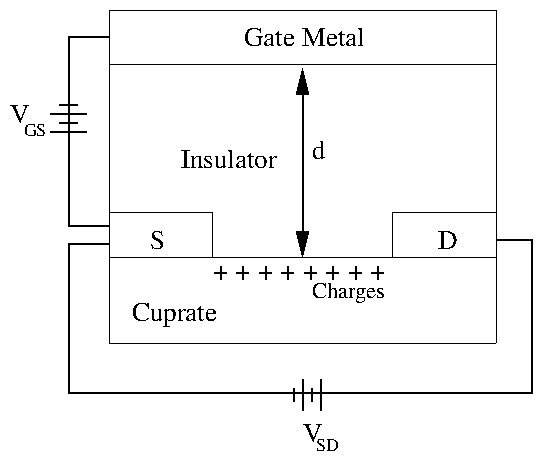
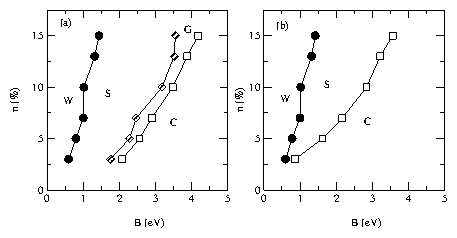
 Figure 2: (a) Phase diagram as a function of the hole density
n and the strength
of the magnetic dipolar interaction B, for a sample without the
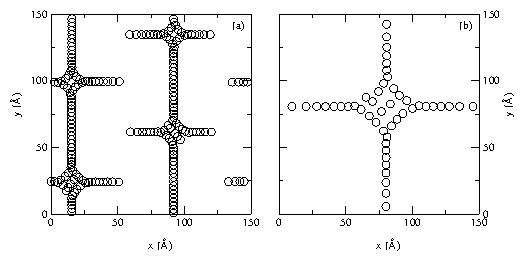
FET interaction term, Eqn. 4. "W" is the Wigner crystal phase,
"S" is the diagonal stripe phase, "G" is the geometric phase,
and "C" is the clump phase. (b) Phase diagram for a sample with the
same parameters but with the
FET interaction added at an insulator thickness of 14Å, showing the
downward shift in B of the clump phase "C," and the suppression of the
geometric phase "G".
Figure 2: (a) Phase diagram as a function of the hole density
n and the strength
of the magnetic dipolar interaction B, for a sample without the
FET interaction term, Eqn. 4. "W" is the Wigner crystal phase,
"S" is the diagonal stripe phase, "G" is the geometric phase,
and "C" is the clump phase. (b) Phase diagram for a sample with the
same parameters but with the
FET interaction added at an insulator thickness of 14Å, showing the
downward shift in B of the clump phase "C," and the suppression of the
geometric phase "G".
|