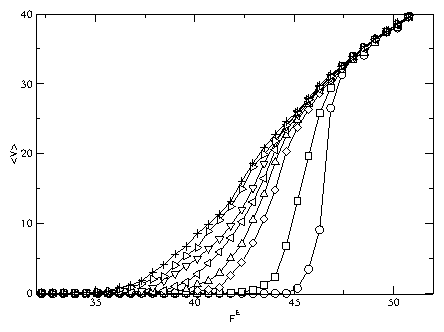
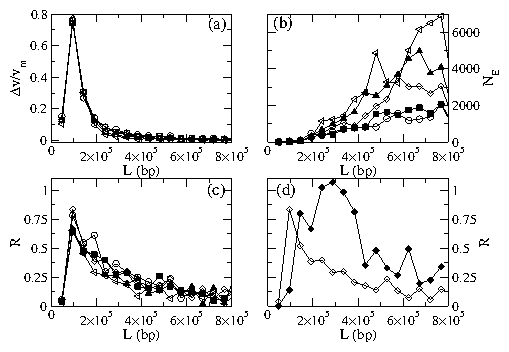
 Figure 7:
(a) Selectivity ∆V/Vm from the system in Fig. 6(a)
versus polymer length L for fp=60
and ρp=0.8 at
FE= 37.88 (circles), 39.0 (squares), 40.12 (diamonds),
41.24 (triangle up), and 42.36 (triangle left).
(b) Efficiency NE for the same system at
FE= 37.88 (open circles), 39.0 (filled squares), 40.12 (diamonds),
41.24 (filled triangle up), and 42.36 (triangle left).
(c) Resolution R for the same system at
FE= 37.88 (open circles), 39.0 (filled squares), 40.12 (diamonds),
41.24 (filled triangle up), and 42.36 (triangle left).
(d) Resolution at FE= 40.12 for: (open diamonds)
the system in Fig. 6(a) and
(filled diamonds) the system in Fig. 6(b) where the polymers
were allowed to travel a longer distance.
Figure 7:
(a) Selectivity ∆V/Vm from the system in Fig. 6(a)
versus polymer length L for fp=60
and ρp=0.8 at
FE= 37.88 (circles), 39.0 (squares), 40.12 (diamonds),
41.24 (triangle up), and 42.36 (triangle left).
(b) Efficiency NE for the same system at
FE= 37.88 (open circles), 39.0 (filled squares), 40.12 (diamonds),
41.24 (filled triangle up), and 42.36 (triangle left).
(c) Resolution R for the same system at
FE= 37.88 (open circles), 39.0 (filled squares), 40.12 (diamonds),
41.24 (filled triangle up), and 42.36 (triangle left).
(d) Resolution at FE= 40.12 for: (open diamonds)
the system in Fig. 6(a) and
(filled diamonds) the system in Fig. 6(b) where the polymers
were allowed to travel a longer distance.
|