Coarsening and Persistence

When a spatially extended system is quenched from a homogeneous high-temperature disordered state to a low temperature state, domains of ordered phases form on larger and larger scales. Although a scale-invariant behavior underlies the spatial structure, additional relaxation laws, characterized by nontrivial scaling exponents, describe more subtle properties such as persistence, i.e., the fraction of the system frozen in its initial state. This behavior, originally found in the kinetic Ising model, is exhibited in systems as diverse as surface growth and interacting particles and as fundamental as the diffusion equation. Experimental studies of liquid crystals, noble gases, and soap films support the theoretical predictions.

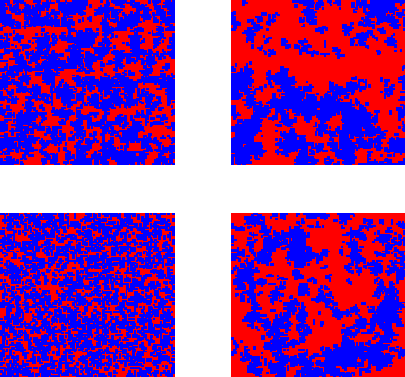
A snapshot of a realization of the voter model at times 1,10,100,1000 on a square lattice of size 100x100. In this exactly solvable model there are two opinions "red" and "blue". All sites continuously change their opinion to that of a randomly chosen neighbor. This model exhibits coarsening in dimensions less or equal than two. In the critical dimension, the perimeter of the interface decreases as an inverse logarithm of time.