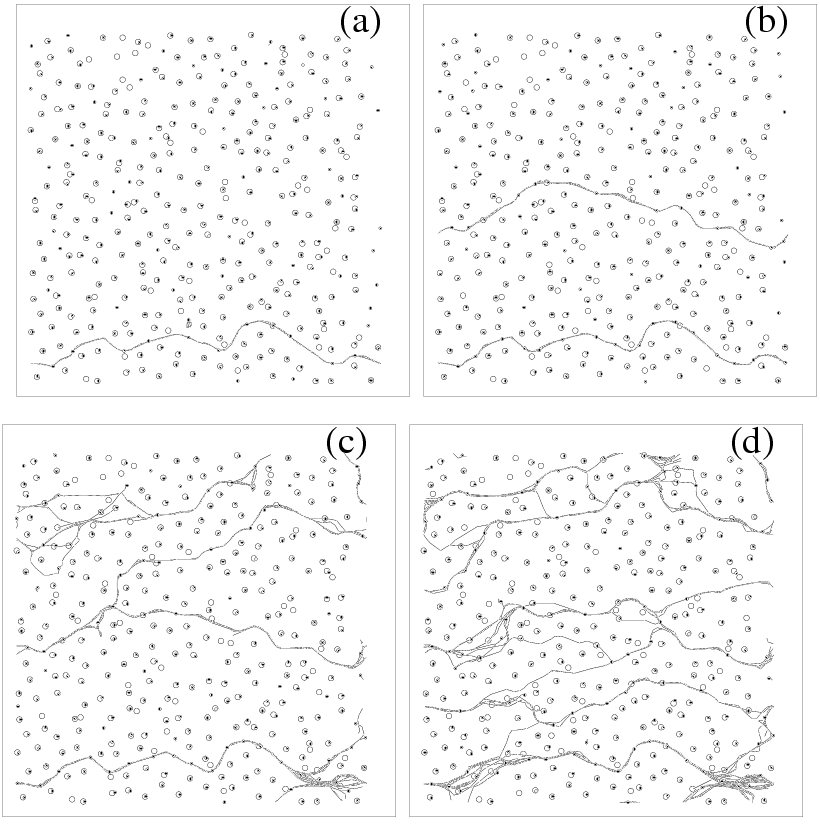
Superconducting vortices in two dimensions

Ideal superconductors carry current without resistance and perfectly expel externally applied magnetic fields. The superconductivity is destroyed when too great a magnetic field is applied, and the material becomes a normal resistive conductor. Type-II materials remain superconducting in high magnetic fields by allowing the magnetic flux to penetrate the material in the form of discrete quantized vortices which repel each other and interact with defects in the superconducting material. The superconducting material returns to its normal resistive state only at the center of these vortices; the remainder of the material still carries a supercurrent. The vortices experience a Lorentz force from the flowing current and move through the superconductor until they are trapped, or pinned, at defect sites. Using molecular dynamics simulations, we explore the microscopic dynamics of vortices interacting with pinning sites under many conditions.

• Avalanche dynamics.
  
• Vortex voltage noise
  
• Vortex rivers: tortuosity and noise
  

Papers:

1. Reversible to irreversible flow transition in periodically driven vortices
   N. Mangan, C. Reichhardt and C.J. Olson Reichhardt
   Phys. Rev. Lett 100 187002 (2008).
   Online version

   LI> Statics and dynamics of vortex liquid crystals
   C. Reichhardt and C.J. Olson Reichhardt
   Euruphys. Lett 75 489 (2006).
   Online version

2. Dynamical behaviors of quasi-one-dimensional vortex states: Possible applications to the vortex chain state
   C. Reichhardt and C.J. Olson Reichhardt
   Phys. Rev. B 66, 172504 (2002).
   Online version

3. Critical depinning force and vortex lattice order in disordered superconductors
   C.J. Olson, C. Reichhardt, and S. Bhattacharya
   Phys. Rev. B 64, 024518 (2001).
   Online version

4. Transverse depinning in strongly driven vortex lattices with disorder
   C.J. Olson and C. Reichhardt
   Phys. Rev. B 61, R3811 (2000).
   Online version

5. Dynamic vortex phases and pinning in superconductors with twin boundaries
   C. Reichhardt, C.J. Olson, and F. Nori
   Phys. Rev. B 61, 3665 (2000).
   Online version

6. Topological invariants in microscopic transport on rough landscapes: Morphology, hierarchical structure, and Horton analysis of riverlike networks of vortices
   A.P. Mehta, C. Reichhardt, C.J. Olson, and F. Nori
   Phys. Rev. Lett. 82, 3641 (1999).
   Online version

7. Nonequilibrium dynamic phase diagram for vortex lattices
   C.J. Olson, C. Reichhardt, and F. Nori
   Phys. Rev. Lett. 81, 3757 (1998).
   Online version

8. Fractal networks, braiding channels, and voltage noise in intermittently flowing rivers of quantized magnetic flux
   C.J. Olson, C. Reichhardt, and F. Nori
   Phys. Rev. Lett. 80, 2197 (1998).
   Online version

9. Plastic flow, voltage noise and vortex avalanches in superconductors
   C.J. Olson, C. Reichhardt, J. Groth, S.B. Field, and F. Nori
   Physica C 290, 89 (1997).
   Online version

10. Superconducting vortex avalanches, voltage bursts, and vortex plastic flow: Effect of the microscopic pinning landscape on the macroscopic properties
    C.J. Olson, C. Reichhardt, and F. Nori
    Phys. Rev. B 56, 6175 (1997).
    Online version

11. Vortex plastic motion in twinned superconductors
    J. Groth, C. Reichhardt, C.J. Olson, S.B. Field, and F. Nori
    Phys. Rev. Lett. 77, 3625 (1996).
    Online version

12. Microscopic derivation of magnetic-flux-density profiles, magnetization hysteresis loops, and critical currents in strongly pinned superconductors
    C. Reichhardt, C.J. Olson, J. Groth, S. Field, and F. Nori
    Phys. Rev. B 52, 10441 (1995).
    Online version

Collaborators

Stuart Field (Colorado State)

Back to Home
Last Modified: 1/1/03