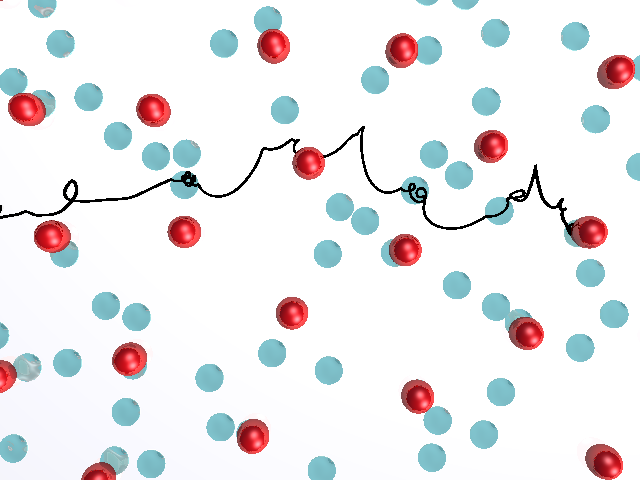
Skyrmions are topological objects with particle-like features that were originally proposed as a model for baryons. Skyrmions also arise in condensed matter systems and in 2009 were discovered in chiral magnets where a triangular skyrmion lattice was observed. Since then, they have been found in numerous materials and show a rich variety of equilibrium and nonequilibrium behaviors, making them promising for a variety of applications. We study skyrmion states using both continuum-based models of the Landau-Lifshitz-Gilbert equation for spin as well as particle-based models in which the skyrmions are represented as effective point particles governed by a derived equation of motion. Specific problems we study include skyrmion motion in random and nanostructured substrates, where the skyrmions can be driven with dc or ac currents, oscillating magnetic fields, or thermal gradients. A particularly interesting aspect of skyrmion dynamics is the role of the Magnus term, which is relatively weak for other systems such as vortices in superconductors, but which for skyrmions can be the dominant contribution to the motion, producing novel dynamical effects that are not observed in other systems. In the first figure above we show the skyrmion and pinning site locations where we highlight the trajectory of a single skyrmion. Here the Magnus term induces swirling dynamics. In the next figure we show results from our continuum model of skyrmions interacting with a square array of defects. When the number of skyrmions is twice the number of defect sites, a square skyrmion lattice can be stabilized. On the other hand, at incommensurate fillings the competition between the skyrmion-skyrmion interactions, which favor a triangular skyrmion lattice, and the skyrmion-substrate interactions, which favor a square skyrmion lattice, produce a disordered skyrmion state.

Back to Home
Last Modified: 5/21/15