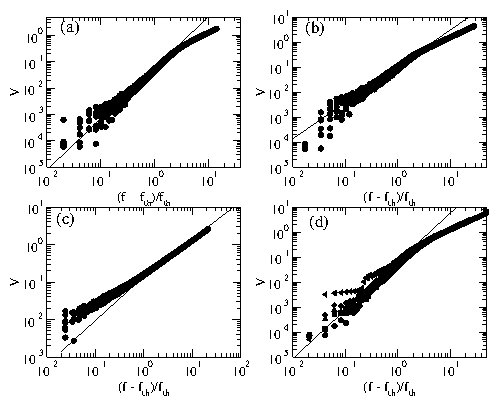
 Figure 1:
The scaling of the average velocity V vs applied drive f for
(a) a 2D system with a fit of ζ = 1.94
(solid line) with nine disorder realizations
and (b) a system of dimension 5 ×500
with a ζ = 1.45 fit (solid line), for eight disorder realizations.
fth is the threshold force at which depinning occurs.
(c) A system geometry of 1 ×500, showing
a fit with ζ = 1.0 (solid line) for nine disorder realizations.
(d) 2D systems for sizes 16 ×16 (triangle left),
30 ×30 (triangle up), 38 ×38 (diamond), 50 ×50
(square), and 60 ×60 (circle). The solid line is a ζ = 1.94
fit.
Figure 1:
The scaling of the average velocity V vs applied drive f for
(a) a 2D system with a fit of ζ = 1.94
(solid line) with nine disorder realizations
and (b) a system of dimension 5 ×500
with a ζ = 1.45 fit (solid line), for eight disorder realizations.
fth is the threshold force at which depinning occurs.
(c) A system geometry of 1 ×500, showing
a fit with ζ = 1.0 (solid line) for nine disorder realizations.
(d) 2D systems for sizes 16 ×16 (triangle left),
30 ×30 (triangle up), 38 ×38 (diamond), 50 ×50
(square), and 60 ×60 (circle). The solid line is a ζ = 1.94
fit.
|
